|
DOI: 10.25136/2409-8671.2017.3.23674
Received:
24-07-2017
Published:
04-09-2017
Abstract:
Mathematical model of geopolitics is a conditional name of several models, which are naturally connected with and serve as companions to the main theme – geopolitics. The author introduces the central notion of a mathematical model of geopolitics – capacity of a habitat. Geopolitics includes climate, terrain, peculiarities of logistics of global flows of commodities, and geopolitical confrontation in terms of “sea – continent”, i.e. all those things composing the material set of conditions of existence of the population of the world. This set to a significant extent mediates political behavior of people. The author doesn’t adhere to the position of environmental determinism in the form of geopolitics, but tries to outline manifestations of geopolitics in the real politics. In all the demonstrated mathematical models, the author refers to a computational experiment, the results of which are presented and discussed in the text. The computational experiment is based on the data about climate, terrain, population and other components typical for modern geo-information systems. The mathematics of these models implies knowing the fundamentals: numerical methods, statistics, methods of optimization and some other disciplines. The author describes the density of habitat capacity in different countries. Par for the course, the top positions are taken by, in decreasing order, Russia, the USA, Brazil, China, Australia. The author defines and studies the index of specific capacity of habitat per capita, ranks countries and territories according to this index. Special attention is given to the correlation between these indexes in particular countries compared to Russia. The author studies the issue of interaction between the density of habitat capacity and terrain, compares territories concentrating 50% of the population and 50% of density of habitat capacity, and outlines the density gradient margins. The author classifies countries and territories in terms of “high – low” and “favourable – unfavourable”, i.e. in four categories taking account of terrain and density of habitat capacity. The paper contains the maps of territories of all four types. The author introduces and calculates the diversity index of particular territories and countries. Within the global traffic calculation, the author creates a specific index of percentage “sea – continent”. Based on this index, the author classifies points (territories) in geopolitical terms. This index helps formalize such well-known geopolitical notions as “Heartland” and “Rimland”. The author composes combined global and regional maps with political and geopolitical marking. These maps are analyzed for so-called geopolitical splits. Such splits are detected when some geopolitical lines don’t coincide with the state border, but lay deeply across its territory. The author demonstrates the numerical solution of the problem of optimal distribution of points (in terms of minimal transportation expenses) serving as logistics hubs on the planet.
Keywords:
capacity of habitat, density of population, minimax transport doctrine, terrain, correlation analysis, Monte Carlo method, territories diversity index, cutting of territories, geopolitical classification of points, non-linear optimization
This article written in Russian. You can find original text of the article here
.
1. Введение
В ряде работ автора [1 – 3] сформулирована “Нормативная модель глобальной истории”. В основе данной модели лежит представление глобальной политической целостности в виде набора атомарных субъединиц, названных геопатомами (ГЕОПолитические АТОМы). Представляется, что текущее политическое строение территорий проживания людей на Земле, в значительной степени, может быть объяснено путем объединения специально приготовленных более мелких территорий — геопатомов. В связи с данной гипотезой возникает задача построения набора геопатомов, покрывающих всю территорию Земли.
Для адекватной нарезки территории Земли на отдельные геопатомы необходимо учесть климатические особенности территорий, а также рельеф. Кроме того, необходимо также учесть глобальный трафик, который заметно меняет конфигурацию расположения и форму геопатомов.
Для учета климатических особенностей проживания на тех или иных территориях будет сформулировано понятие “емкость среды обитания”. Будет построена подходящая функция плотности емкости среды обитания, которая включит в себя весь комплекс антропоморфных требований к среде обитания в части климата. Территории проживания людей будут классифицированы в терминах “(не)высоко – (не)благоприятно”, т.е. с учетом высоты над уровнем моря и климатических особенностей.
В части моделирования глобального трафика особенно остро проявится центральное геополитическое противостояние между “морем” и “континентом”, о чем предупреждали классики геополитики. Формулировка алгоритма и подсчет с его помощью глобальных транспортных потоков позволит уточнить и обобщить классификацию всех территорий в общепринятых геополитических категориях.
2. Емкость среды обитания
Построим математическую модель того, что называют по-разному в разных дисциплинах: емкость среды обитания, жизненное пространство и пр. Нас будет интересовать построение меры объема среды обитания путем учета различного рода наиболее важных природных составляющих, сопровождающих жизнь людей. К таким составляющим отнесем, прежде всего, среднегодовые значения температуры и осадков на поверхности Земли.
Пространственную развертку в модели свяжем с координатами широты, 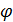 и долготы, и долготы, 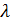 поверхности Земли, считая, что поверхности Земли, считая, что 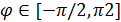 , , 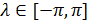 — в радианах или — в радианах или 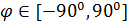 , , 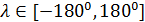 — в градусах. Для подбора подходящей формулы связи плотности емкости среды обитания, — в градусах. Для подбора подходящей формулы связи плотности емкости среды обитания, 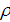 с среднегодовой температурой с среднегодовой температурой 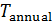 и осадками и осадками  привлечем реальные данные, имеющиеся для всей поверхности Земли. привлечем реальные данные, имеющиеся для всей поверхности Земли.
Введем комфортные с точки зрения проживания людей значения температуры,  и осадков, и осадков, 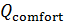 согласно средневзвешенной процедуре, выбирая в качестве веса плотность проживания людей на поверхности Земли, согласно средневзвешенной процедуре, выбирая в качестве веса плотность проживания людей на поверхности Земли,  . В этом случае можно записать следующую общую формулу для подс—чета . В этом случае можно записать следующую общую формулу для подс—чета  и и 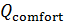 : :
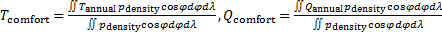 , (1) , (1)
где 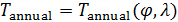 , , 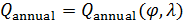 , , 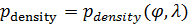 — соответствующие функции широты и долготы; интегрирование в (1) предполагается по всему глобусу без учета водной поверхности. — соответствующие функции широты и долготы; интегрирование в (1) предполагается по всему глобусу без учета водной поверхности.
Выберем разрешение по пространству в 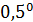 градусов и рассмотрим конкретные данные для среднегодовых значений температуры, осадков и плотности населения. В этом случае данные предстанут в виде матриц размером градусов и рассмотрим конкретные данные для среднегодовых значений температуры, осадков и плотности населения. В этом случае данные предстанут в виде матриц размером 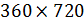 , где 360 обозначает количество узлов равномерной сетки по широте, а 720 — по долготе. Сетки по широте и долготе в радианах можно представить в виде: , где 360 обозначает количество узлов равномерной сетки по широте, а 720 — по долготе. Сетки по широте и долготе в радианах можно представить в виде: 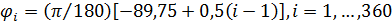 ; ; 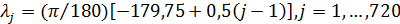 . .
Загрузим данные по среднегодовым значениям температуры и осадков с сайта [4]. Выберем версию архива 2.02, которая датирована июлем 2001 года. Описание к данным архива приведено на сайте [5]. Данные по плотности населения Земли возьмем с сайта NASA Earth Observations [6]. Заменим интегрирование в (1) суммированием по нашей сетке, тогда
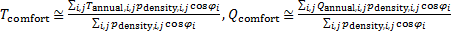 , (2) , (2)
где суммирование в (2) осуществляется по тем узлам сетки, которые не принадлежат водной поверхности.
По формуле (2) был проведен расчет с данными из архива 2.02 и данными NASA по плотности населения, оказалось, что 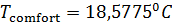 ; ; 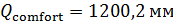 . .
Были подсчитаны также средневзвешенные стандартные отклонения от комфортных значений, они оказались равными 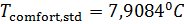 и и 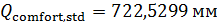 соответственно для температуры и осадков. Столь заметные стандартные отклонения означают, что предполагаемая зависимость емкости среды r от отклонений от комфортных значений в форме степенных выражений типа соответственно для температуры и осадков. Столь заметные стандартные отклонения означают, что предполагаемая зависимость емкости среды r от отклонений от комфортных значений в форме степенных выражений типа 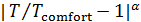 и и  должна иметь малые по сравнению с единицей значения степеней должна иметь малые по сравнению с единицей значения степеней 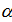 и и 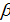 . .
После ввода комфортных значений температуры и осадков, выберем для дальнейшего анализа следующую формулу для описания плотности емкости среды обитания:
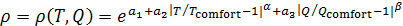 , (3) , (3)
где 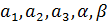 — пока неопределенные константы. — пока неопределенные константы.
В представлении (3) сосредоточен весь набор требований к функции 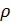 . Функция, описывающая емкость среды, . Функция, описывающая емкость среды, 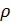 должна быть неотрицательной, зависеть от отклонений от комфортных значений, легко модифицируемой в случае учета дополнительного параметра, описывающего емкость среды. должна быть неотрицательной, зависеть от отклонений от комфортных значений, легко модифицируемой в случае учета дополнительного параметра, описывающего емкость среды.
Неопределенные параметры 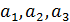 , входящие в (3) найдем путем минимизации суммы квадратов отклонений обратной функции емкости среды, , входящие в (3) найдем путем минимизации суммы квадратов отклонений обратной функции емкости среды, 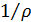 от обратной функций плотности народонаселения, от обратной функций плотности народонаселения,  . Выяснилось, что именно в этом случае обеспечивается максимум корреляции величины обратной функции емкости среды и обратной величины плотности населения, . Выяснилось, что именно в этом случае обеспечивается максимум корреляции величины обратной функции емкости среды и обратной величины плотности населения, 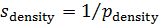 . Величина . Величина 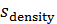 имеет ясный географический смысл — это количество квадратных километров, приходящихся на одного человека в данном регионе, если имеет ясный географический смысл — это количество квадратных километров, приходящихся на одного человека в данном регионе, если  измеряется в количестве людей на квадратный километр. измеряется в количестве людей на квадратный километр.
С учетом (1) запишем функционал, D минимум которого обеспечивает поиск параметров 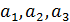 при фиксированных значениях при фиксированных значениях 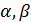 : :
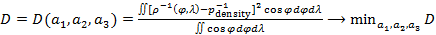 , (4) , (4)
где интегрирование предполагается по всей суше, без учета водной поверхности.
Учитывая (2), перепишем функционал (4) в конечно-разностном виде, исходя, как и выше, из разрешения в 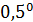 . В этом случае, с точностью до численного коэффициента, получим . В этом случае, с точностью до численного коэффициента, получим
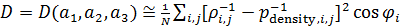 , (5) , (5)
где 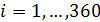 ; ; 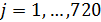 ; ;  — количество узлов сетки на поверхности суши, а суммирование распространяется лишь на те узлы сетки, которые приходятся на сушу. — количество узлов сетки на поверхности суши, а суммирование распространяется лишь на те узлы сетки, которые приходятся на сушу.
Для поиска минимума функционала в форме (5) решалась задача градиентного спуска
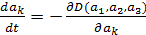 , , 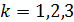 , (6) , (6)
где 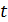 — некоторый условный аргумент, при этом — некоторый условный аргумент, при этом
 , ,
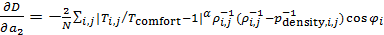 , ,
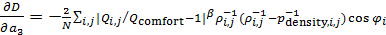 . .
Система дифференциальных уравнений (6) может быть решена с помощью одного из стандартных решателей, например, пакета MATLAB. Решение проводилось вплоть до установления значений 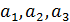 , т.е. когда можно отчетливо идентифицировать наличие пределов значений , т.е. когда можно отчетливо идентифицировать наличие пределов значений 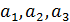 при при 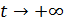 . .
В таблице №1 приведен перечень значений параметров, входящих в формулу (3) для емкости среды, полученный с учетом решения задач (2), (5), (6). Кроме того, в таблице №1 приведены соответствующие значения коэффициента корреляции, Corr, который устанавливает связь между наборами 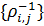 и и 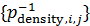 , i = 1,…,360; j = 1,…,720. С учетом особенностей геометрии на сфере, корреляция подсчитывалась по формуле: , i = 1,…,360; j = 1,…,720. С учетом особенностей геометрии на сфере, корреляция подсчитывалась по формуле:
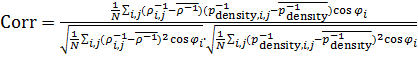 , (7) , (7)
где
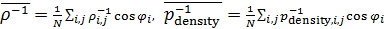 . .
|
Таблица №1. Перечень значений параметров, входящих в формулу емкости среды обитания
|
|
№№
|

|
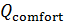
|
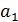
|
|
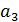
|
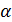
|

|
Corr
|
|
1
|
18,5775
|
1200,2
|
0,7156
|
–0,0649
|
–0,0426
|
2
|
2
|
0,5758
|
|
2
|
18,5775
|
1200,2
|
1,0227
|
–0,2767
|
–0,2991
|
1
|
1
|
0,6329
|
|
3
|
18,5775
|
1200,2
|
1,6592
|
–0,6627
|
–0,6656
|
0,5
|
0,5
|
0,6581
|
|
4
|
18,5775
|
1200,2
|
6,2794
|
–3,2566
|
–2,7573
|
0,1
|
0,1
|
0,6590
|
|
5
|
18,5775
|
1200,2
|
3,4189
|
–1,6624
|
–1,4789
|
0,2
|
0,2
|
0,6611
|
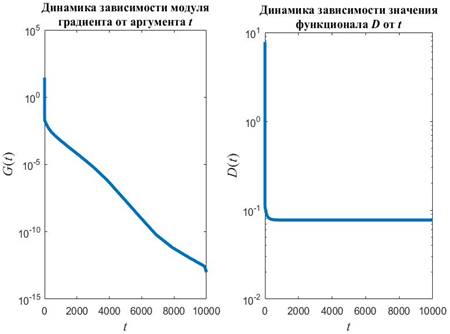
Рис.1. Динамика зависимости модуля градиента G (левый график) и значения функционала D (правый график) от аргумента t
На рис.1 приведены типичные образцы зависимости модуля градиента 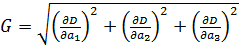 и значения функционала (5), D от аргумента t. Графики рис.1 демонстрируют очевидную сходимость модуля градиента G к нулю (левый график), а значение функционала D к некоторому предельному, минимальному значению (правый график). Это означает, что набор параметров и значения функционала (5), D от аргумента t. Графики рис.1 демонстрируют очевидную сходимость модуля градиента G к нулю (левый график), а значение функционала D к некоторому предельному, минимальному значению (правый график). Это означает, что набор параметров 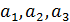 сходится к своим предельным значениям при сходится к своим предельным значениям при 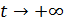 . Остальные значения параметров выбирались согласно пункту №5 таблицы №1, когда имело место максимальное значение корреляции. . Остальные значения параметров выбирались согласно пункту №5 таблицы №1, когда имело место максимальное значение корреляции.
Отрицательные значения знаков параметров 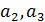 в таблице №1 отвечают нашим ожиданиям. Варьированию подвергались значения параметров в таблице №1 отвечают нашим ожиданиям. Варьированию подвергались значения параметров 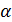 и и  . Оказалось, что максимальное значение корреляции без учета более мелких вариаций находится в окрестности значений степеней . Оказалось, что максимальное значение корреляции без учета более мелких вариаций находится в окрестности значений степеней 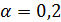 и и 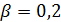 . Отметим, что если в формуле для емкости среды (3) не учитывать осадки ( . Отметим, что если в формуле для емкости среды (3) не учитывать осадки ( ), коэффициент корреляции при значении параметров из пункта №5 таблицы №1 составит значение 0,6341. Полученное значение несколько меньше числа 0,6611, т.е. компонента осадков дает свой вклад. Наконец, в случае отсутствия температуры в формуле (3) ( ), коэффициент корреляции при значении параметров из пункта №5 таблицы №1 составит значение 0,6341. Полученное значение несколько меньше числа 0,6611, т.е. компонента осадков дает свой вклад. Наконец, в случае отсутствия температуры в формуле (3) ( ) значение корреляции составило 0,5587, что заметно меньше значения 0,6611. Данные замечания означают, что совместное использование показателей температуры и осадков повышает корреляцию значений обратной функции емкости среды обитания и обратной функции плотности народонаселения. Таким образом, можно сделать вывод о том, что приблизительно две трети корреляции между обратной функцией емкости среды обитания, вычисляемой по формуле (3) и функцией обратной плотности народонаселения приходится на среду обитания в части температуры и осадков. ) значение корреляции составило 0,5587, что заметно меньше значения 0,6611. Данные замечания означают, что совместное использование показателей температуры и осадков повышает корреляцию значений обратной функции емкости среды обитания и обратной функции плотности народонаселения. Таким образом, можно сделать вывод о том, что приблизительно две трети корреляции между обратной функцией емкости среды обитания, вычисляемой по формуле (3) и функцией обратной плотности народонаселения приходится на среду обитания в части температуры и осадков.
Сравним визуально карты обратной функции плотности емкости среды обитания и обратной функции плотности народонаселения. Искомые карты нарисуем с помощью линий уровня. На рис.2 приведен итог. На левой карте рис.2 приведены линии уровня обратной функции плотности емкости среды, рассчитанной по формуле (3) с параметрами из пункта №5 таблицы №1. Всего построено 12 линий уровня с равноотстоящими значениями, которые отображают диапазон изменения обратной емкости [0,0054;1,1268]. На правой карте рис.2 приведена обратная функция плотности народонаселения. Построено также 12 линий уровня с равноотстоящими значениями, которые отображают диапазон изменения обратной плотности народонаселения [0,0001;0,9664].
На рис.2 все более синим вплоть до фиолетового цветами обозначены места малых значений обратной функции плотности емкости среды и обратной функции народонаселения. Видна явная корреляция местоположений синих и фиолетовых мест на левой и правой картах рис.2. Отметим, что данные места отвечают наиболее комфортным для человека условиям проживания. Имеются и заметные расхождения на всех континентах. Справа от каждой из карт приведена палитра, устанавливающая связь с численным значением соответствующего показателя. Кроме того, на каждой из карт проведена береговая линия в виде красной линии.

Рис.2. Карты линий уровня функции обратной плотности емкости среды обитания (слева) и обратной функции плотности народонаселения (справа)
Перейдем от обратных значений плотности емкости среды и плотности народонаселения к прямым значениям. Сравним линейный коэффициент корреляции Пирсона и ранговые корреляции Кендалла и Спирмена для плотности емкости среды обитания и плотности народонаселения. Для этого преобразуем матрицы 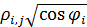 и и 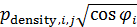 в векторы и найдем между этими векторами соответствующие коэффициенты корреляции. В таблице №2 приведен итог. в векторы и найдем между этими векторами соответствующие коэффициенты корреляции. В таблице №2 приведен итог.
|
Таблица №2. Коэффициенты корреляции Пирсона, Кендалла и Спирмена между плотностью емкости среды обитания и плотностью народонаселения
|
|
Коэфф. корр.
|
Пирсона
|
Кендалла
|
Спирмена
|
|
Значение коэфф. корр.
|
0,1740
|
0,7582
|
0,9034
|
Из таблицы №2 видно сколь велики коэффициенты ранговой корреляции по сравнению с обычным линейным коэффициентом корреляции. Именно по этой причине в (7) рассматривался линейный коэффициент корреляции между обратными функциями плотности емкости среды обитания и плотности народонаселения. Для обратных величин линейный коэффициент корреляции оказался равным 0,6611, что значительно больше значения 0,1740.
В итоге проведенных выше построений и вычислений выберем для функции емкости среды обитания людей функцию (3), которая отображает связь с такими характеристиками, как температура и осадки, а точнее с отклонениями температуры и осадков от соответствующих комфортных значений.
3. Развертка емкости среды обитания по государствам
Учитывая функциональное представление для емкости среды обитания (3), запишем формулу для подсчета глобальной емкости среды обитания:
 . (8) . (8)
В начале найдем центр сосредоточения или центр рассеяния емкости среды обитания и сравним его с центром рассеяния народонаселения Земли. Перейдем к дискретному представлению всех интегральных показателей, исходя из сетки по широте и долготе размером 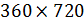 . Подсчитаем центр рассеяния народонаселения согласно формулам: . Подсчитаем центр рассеяния народонаселения согласно формулам:
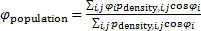 , , 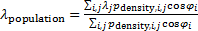 , (9) , (9)
где суммирование распространяется на те пары 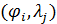 , , 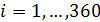 ; ; 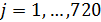 , которые принадлежат суше. Плотность народонаселения , которые принадлежат суше. Плотность народонаселения 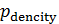 выберем, подобной предыдущему разделу. выберем, подобной предыдущему разделу.
Аналогично формулам (9) определим выражения для подсчета центра рассеяния емкости среды обитания:
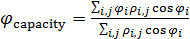 , , 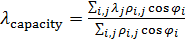 , (10) , (10)
где 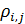 , , 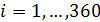 ; ; 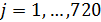 — плотность емкости среды обитания (3) со значениями параметров из пункта №5 таблицы №1. — плотность емкости среды обитания (3) со значениями параметров из пункта №5 таблицы №1.
|
|
|
|
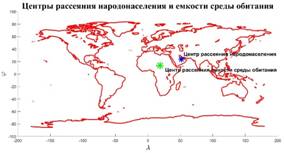
Рис.3,а. Центры рассеяния народонаселения (Аравийский полуостров) и емкости среды обитания (Центральная Африка)
|
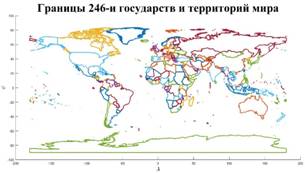
Рис.3,б. Границы 246-и государств и территорий мира
|
На рис.3,а приведен итог подсчета центров рассеяния народонаселения, 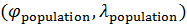 и емкости среды обитания, и емкости среды обитания, 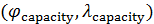 . Оказалось, что центр рассеяния народонаселения имеет координаты (23,78 с.ш.; 51,85 в.д.) — Аравийский полуостров, Саудовская Аравия, солончаки. Центр рассеяния емкости среды обитания имеет координаты (13,59 с.ш.; 19,03 в.д.) — Центральная Африка, Центральный Чад, восточнее г. Нджамены. . Оказалось, что центр рассеяния народонаселения имеет координаты (23,78 с.ш.; 51,85 в.д.) — Аравийский полуостров, Саудовская Аравия, солончаки. Центр рассеяния емкости среды обитания имеет координаты (13,59 с.ш.; 19,03 в.д.) — Центральная Африка, Центральный Чад, восточнее г. Нджамены.
Отметим, что в модели, как размерность, так и абсолютное значение емкости среды обитания не существенно. Важна лишь пространственная развертка, т.е. относительные значения емкости среды обитания либо отдельных регионов, либо значений плотности среды отдельных точек.
В качестве примера подсчета глобальной емкости среды обитания (8) рассмотрим политическую карту мира с границами отдельных государств и территорий и подсчитаем емкость среды обитания для каждого из государств и территорий. По данным ООН на 2008 г. отмечены границы 246-и государств и территорий, данные о которых представлены, например, на сайте [7]. На рис.3,б приведена графическая иллюстрация всех имеющихся на 2008 г. границ государств и территорий.
Определим область, занимаемую  -м государством или территорией, символом -м государством или территорией, символом 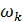 . В этом случае глобальную емкость среды обитания (8) с учетом выбранной разметки поверхности Земли можно переписать в виде: . В этом случае глобальную емкость среды обитания (8) с учетом выбранной разметки поверхности Земли можно переписать в виде:
 (11) (11)
Для вычисления емкости среды обитания всех государств и территорий 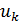 , ,  заменим двойные интегралы в (11) на приближенные суммы, исходя из разрешения в половину градуса по широте и долготе. В этом случае второе уравнение в (11) можно переписать в виде: заменим двойные интегралы в (11) на приближенные суммы, исходя из разрешения в половину градуса по широте и долготе. В этом случае второе уравнение в (11) можно переписать в виде:
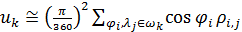 , (12) , (12)
где 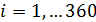 , , 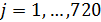 , а суммирование в (12) распространяется на те точки , а суммирование в (12) распространяется на те точки 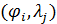 , которые входят в область , которые входят в область 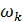 . .
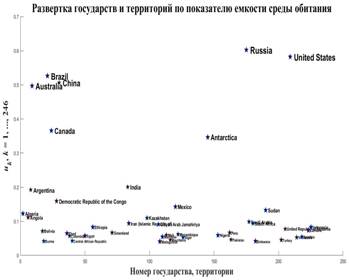
Рис.4. Развертка государств и территорий по показателю емкости среды обитания
Был проведен вычислительный эксперимент по подсчету набора емкостей среды обитания государств и территорий (12), при этом матрица 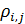 вычислялась по формуле (3) с параметрами из пункта №5 таблицы №1. вычислялась по формуле (3) с параметрами из пункта №5 таблицы №1.
На рис.4 приведен итоговый график, на котором помечены некоторые страны и территории развернутые по показателю емкости среды обитания. В частности, первая пятерка по показателю емкости среды обитания в порядке убывания выглядит следующим образом: Россия, США, Бразилия, Китай, Австралия со значениями показателя 0,6027; 0,5818; 0,5261; 0,5061; 0,4968 соответственно.
Глобальная емкость среды обитания  составила величину 7,6438, при этом среднее значение — 0,0311, а стандартное отклонение — 0,0863. составила величину 7,6438, при этом среднее значение — 0,0311, а стандартное отклонение — 0,0863.
Изучим распределение емкости среды обитания, приходящейся на одного человека. Введем подходящую переменную в следующем виде:
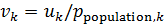 , (13) , (13)
где  — народонаселение — народонаселение  -го государства или территории, -го государства или территории,  . Переменная . Переменная  , введенная в (13), обозначает объем среды обитания, приходящейся на одного человека в пределах , введенная в (13), обозначает объем среды обитания, приходящейся на одного человека в пределах  -го государства или территории или удельное значение объема среды обитания. В качестве конкретных значений народонаселения были выбраны данные за 2005 г., которые приведены там же, где и данные границ 246-и государств и территорий. -го государства или территории или удельное значение объема среды обитания. В качестве конкретных значений народонаселения были выбраны данные за 2005 г., которые приведены там же, где и данные границ 246-и государств и территорий.

Рис.5. Развертка государств и территорий по показателю удельной емкости среды обитания
Проведенный расчет набора показателей  , ,  показал, что победителем является Гренландия. На рис.5 приведен график, подобный графику рис.4, где по оси ординат отложены некоторые значения набора удельных объемов среды показал, что победителем является Гренландия. На рис.5 приведен график, подобный графику рис.4, где по оси ординат отложены некоторые значения набора удельных объемов среды  , ,  , нормированных на величину максимального удельного объема , нормированных на величину максимального удельного объема 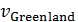 . .
Рассмотрим отношение удельной емкости среды обитания России по отношению к ряду иных государств. В таблице №3 приведен некоторый характерный перечень отношений.
|
Таблица №3. Отношение удельного объема среды обитания РФ к удельным объемам ряда других стран
|
|
РФ/Финляндия
|
РФ/Великобритания
|
РФ/Франция
|
РФ/Германия
|
|
1,5416
|
17,6738
|
7,5665
|
16,6839
|
|
РФ/Польша
|
РФ/Украина
|
РФ/Турция
|
РФ/Казахстан
|
|
10,4924
|
6,8427
|
6,7931
|
0,5802
|
|
РФ/Китай
|
РФ/Япония
|
РФ/США
|
|
|
10,8619
|
23,3693
|
2,1576
|
|
Согласно таблице №3 наибольшие значения отношений удельного объема среды обитания РФ к удельным объемам иных стран приходится на три страны, традиционно входящие в историческую орбиту РФ, это Великобритания, Германия и Япония.
Построим карту, на которой стрелами укажем переходы от тех стран, у которых, с одной стороны, достаточно высокий потенциал емкости среды обитания (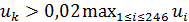 ), с другой стороны, отношение удельной емкости среды обитания РФ к удельной емкости иной страны больше некоторого порогового значения ( ), с другой стороны, отношение удельной емкости среды обитания РФ к удельной емкости иной страны больше некоторого порогового значения ( . Таким образом, учтем лишь те страны, емкость среды обитания которых превышает 2% от емкости самого крупного государства, т.е. РФ. В качестве порогового значения отношений удельной емкости среды обитания РФ и удельных емкостей иных стран выберем значение 7,5, т.е. достаточно высокое значение. . Таким образом, учтем лишь те страны, емкость среды обитания которых превышает 2% от емкости самого крупного государства, т.е. РФ. В качестве порогового значения отношений удельной емкости среды обитания РФ и удельных емкостей иных стран выберем значение 7,5, т.е. достаточно высокое значение.
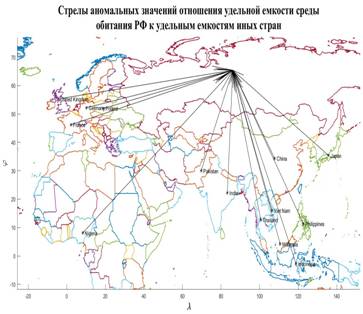
Рис.6. Стрелы аномальных значений отношения удельной емкости среды обитания РФ и удельных емкостей иных стран
На рис.6 приведена карта с искомыми стрелами. При выбранных пороговых значениях емкостей среды обитания и удельных емкостей отдельных государств, оказалось в наличии 13 стрел, которые противоставляют 13 стран с РФ. Часть стран, представленных на рис.6, фигурируют также и в таблице №3. Отметим, что все 13 стрел направлены к РФ.
4. Емкость среды обитания (плотность народонаселения) и рельеф
Используя соответствующие данные, разберемся с плотностью емкости среды обитания (плотностью народонаселения) в связи с рельефом поверхности Земли (данные по рельефу были взяты из раздела Mapping Toolbox пакета MATLAB). Данные по рельефу представим в координатах широта, долгота с разрешением 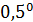 в виде матрицы в виде матрицы 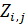 , , 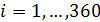 ; ; 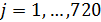 . .
Определим набор средних высот в разных смыслах: среднюю высоту суши, 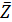 ; средневзвешенную высоту, ; средневзвешенную высоту, 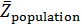 , где в качестве весов выбирается плотность народонаселения; а также средневзвешенную высоту проживания 50% народонаселения, , где в качестве весов выбирается плотность народонаселения; а также средневзвешенную высоту проживания 50% народонаселения,  , когда , когда 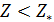 и и 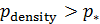 , где , где 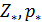 — некоторые неотрицательные константы. Перечисленные выше средние величины найдем согласно следующим формулам: — некоторые неотрицательные константы. Перечисленные выше средние величины найдем согласно следующим формулам:
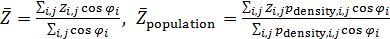 . (14) . (14)
Формула для подсчета величины  аналогична второй формуле из (14) при условии того, что суммирование распространяется по тем парам индексов аналогична второй формуле из (14) при условии того, что суммирование распространяется по тем парам индексов 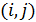 , для которых верны неравенства: , для которых верны неравенства: 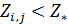 и и 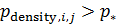 . Пороговые значения . Пороговые значения 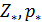 подбирались из тех соображений, чтобы доля народонаселения, проживающая в условиях подбирались из тех соображений, чтобы доля народонаселения, проживающая в условиях 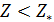 и и 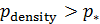 равнялась 50%. Итог расчетов средних величин и параметров приведен в таблице №4. равнялась 50%. Итог расчетов средних величин и параметров приведен в таблице №4.
|
Таблица №4. Набор средних высот и подходящих значений параметров
|
|
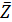
|
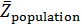
|

|

|
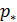
|
|
804,9 м
|
442,9 м
|
61,3 м
|
187,5 м
|
2 чел/км2
|
Согласно таблице №4 средняя высота суши 804,9 метров. Средневзвешенная высота суши с учетом плотности народонаселения, грубо говоря, в два раза меньше, точнее, равна 442,9 м. Наконец, 50% народонаселения проживают в пределах высоты 187,5 м, при этом средневзвешенная высота расселения с учетом плотности народонаселения равняется 61,3 м. Последнее среднее значение характеризует известный факт, что половина народонаселения сосредоточена в окрестности береговой линии мирового океана.
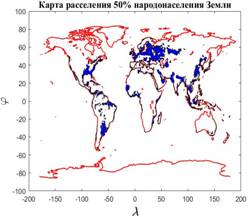
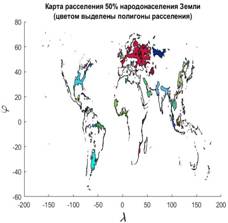
На рис.7 приведены две карты расселения 50% народонаселения, сосредоточенных вблизи береговой кромки и при условии, что плотность народонаселения превышает выбранный порог 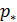 . На карте рис.7,а приведена береговая линия (красного цвета) и области расселения народонаселения (тонированы синим цветом). На карте рис.7,б разными цветами выделены отдельные замкнутые полигоны, отвечающие условиям того, что проживание людей осуществляется на высотах не превышающих значение . На карте рис.7,а приведена береговая линия (красного цвета) и области расселения народонаселения (тонированы синим цветом). На карте рис.7,б разными цветами выделены отдельные замкнутые полигоны, отвечающие условиям того, что проживание людей осуществляется на высотах не превышающих значение  при плотности народонаселения, превышающей значение при плотности народонаселения, превышающей значение 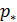 . В данном расчете всего таких полигонов оказалось 932, при этом береговая кромка не нанесена, но она легко просматривается в позициях самих полигонов. . В данном расчете всего таких полигонов оказалось 932, при этом береговая кромка не нанесена, но она легко просматривается в позициях самих полигонов.
|
|
|
|
Рис.7,а. Карта расселения 50% народонаселения Земли (общий ракурс)
|
Рис.7,б. Карта расселения 50% народонаселения Земли (мультиполигональный ракурс)
|
Приведенные выше соображения о взаимосвязи рельефа и плотности расселения народонаселения Земли говорят об их сложной взаимосвязи. В частности, ввести комфортное значение высоты проживания, подобно комфортным значениям температуры и осадков не удается.
Решим задачу идентификации территорий, на которых сосредоточено 50% всей емкости среды обитания  . Данные территории найдем из условия того, что высоты не превышают некоторое пороговое значение . Данные территории найдем из условия того, что высоты не превышают некоторое пороговое значение 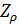 , а плотность емкости среды превышает некоторое пороговое значение , а плотность емкости среды превышает некоторое пороговое значение 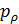 . В качестве плотности емкости среды обитания возьмем функцию (3) с параметрами из пункта №5 таблицы №1. Определим средневзвешенную высоту . В качестве плотности емкости среды обитания возьмем функцию (3) с параметрами из пункта №5 таблицы №1. Определим средневзвешенную высоту 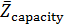 , где в качестве весом выступает плотность емкости среды r, а также средневзвешенную среднюю по территориям, , где в качестве весом выступает плотность емкости среды r, а также средневзвешенную среднюю по территориям,  , где сосредоточено 50% всей емкости среды. Аналогично (14) запишем формулу для расчета средневзвешенной высоты: , где сосредоточено 50% всей емкости среды. Аналогично (14) запишем формулу для расчета средневзвешенной высоты:
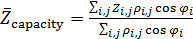 , (15) , (15)
где суммирование в (15) распространяется по тем парам 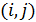 , для которых , для которых  . .
В таблице №5 приведен набор значений параметров, который выступает в виде решения, сформулированной выше задачи.
|
Таблица №5. Набор средневзвешенных высот и подходящих пороговых значений параметров с учетом плотности емкости среды
|
|
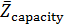
|
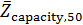
|
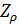
|
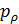
|
U
|
|
714,5 м
|
312,1 м
|
820 м
|
1,82
|
7,7039
|
Параметры, приведенные в таблице №5 позволяют найти территории, на которых сосредоточено 50% емкости среды обитания. Это те территории, которые находятся в пределах высоты 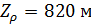 , причем значения плотности емкости среды обитания превышают значение , причем значения плотности емкости среды обитания превышают значение 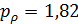 . .
На рис.8 построены карты, которые иллюстрируют позиционирование 741-й территории, подпадающих под указанные ограничения. На левой карте рис.8 искомые территории закрашены одним цветом, а на правой карте — разными цветами.

Рис.8. Карта территорий, несущих 50% емкости среды обитания в разных тонировках: единая тонировка (левая карта) и тонировка территорий разными цветами (правая карта)
Отметим, что карты на рис.7 и рис.8 отличаются довольно существенно. Это можно объяснить следующим образом. Плотность населения Земли, которая была использована в качестве веса в формулах (19), менялась в диапазоне [1,04;104]. Плотность емкости среды обитания, которая использовалась в качестве веса в формуле (20), менялась в диапазоне [0,77;15,26]. Пара диапазонов отличаются друг от друга в 690 раз. Другими словами, народонаселение Земли за счет высокой плотности, т.е. путем сосредоточения в крупных городских агломерациях, “экономит” на пространстве. Кроме того были вычислены площади мест проживания 50% народонаселения, 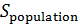 и площадь мест сосредоточения 50% емкости среды обитания, и площадь мест сосредоточения 50% емкости среды обитания,  , представленных на рис.7, 8. Оказалось, что , представленных на рис.7, 8. Оказалось, что 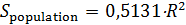 , , 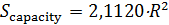 , где , где 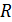 — радиус поверхности Земли. Таким образом, поверхность проживания 50% народонаселения в 4 с лишним раза меньше поверхности позиционирования 50% емкости среды обитания. — радиус поверхности Земли. Таким образом, поверхность проживания 50% народонаселения в 4 с лишним раза меньше поверхности позиционирования 50% емкости среды обитания.
Карты на рис.8 можно проиллюстрировать с другой точки зрения, путем построения поля градиента плотности емкости среды обитания. Определим в сферической системе координат двухкомпонентный вектор-градиент 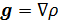 плотности емкости среды обитания в виде: плотности емкости среды обитания в виде:
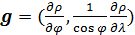 . (16) . (16)
Плотность емкости среды обитания рассмотрим на сетке с разрешением в половину градуса. Для аппроксимации производных в (16) возьмем четырехточечный шаблон, тогда запишем
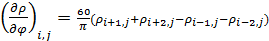 , (17) , (17)
где 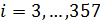 ; ; 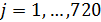 и и
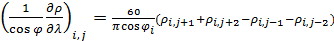 , (18) , (18)
где 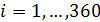 ; ; 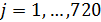 , при этом предполагается в (18) периодическое продолжение по индексу j с периодом 720. , при этом предполагается в (18) периодическое продолжение по индексу j с периодом 720.
На рис.9 в виде набора стрелок приведено поле градиента, 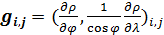 плотности емкости среды, подсчитанного по формулам (16) — (18) с плотностью емкости среды обитания (3) с параметрами из пункта №5 таблицы №1. плотности емкости среды, подсчитанного по формулам (16) — (18) с плотностью емкости среды обитания (3) с параметрами из пункта №5 таблицы №1.
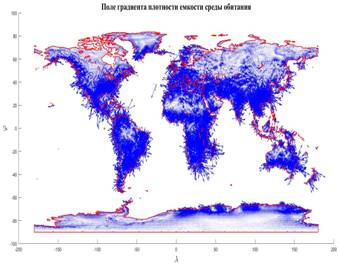
Рис.9. Поле градиента плотности емкости среды обитания
На рис.9 отчетливо в виде “бахромы” стрелок виден заметный рост плотности емкости среды обитания по мере приближения к береговой линии, что еще раз подтверждает известный факт о том, что половина народонаселения Земли проживает в окрестности побережья мирового океана.
5. Нарезка территорий в терминах (не)высоко – (не)благоприятно
Исследования, представленные в предыдущем разделе, позволяют осуществить классификацию, нарезку территорий в терминах “высоко – невысоко”, “благоприятно – неблагоприятно”. Терминология “высоко – невысоко” означает буквально следующее: местность проживания находится на высоте больше некоторого порогового значения 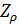 или, соответственно, меньше. Терминология “благоприятно – неблагоприятно” означает, что плотность емкости среды обитания превышает некоторое пороговое значение или, соответственно, меньше. Терминология “благоприятно – неблагоприятно” означает, что плотность емкости среды обитания превышает некоторое пороговое значение 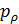 или, соответственно, меньше. или, соответственно, меньше.
По данным предыдущего раздела пороговые значения 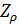 и и 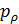 были найдены из того, чтобы емкость среды обитания территорий охваченных этими условиями равнялась 50%. Согласно таблице №5, были найдены из того, чтобы емкость среды обитания территорий охваченных этими условиями равнялась 50%. Согласно таблице №5, 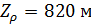 и и 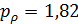 . .
Рассмотрим теперь условное пространство с координатами 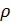 ( (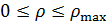 ) и ) и 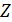 ( ( ) и проведем две линии ) и проведем две линии 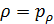 и и 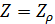 , тогда любая местность обитания на Земле может быть отнесена к одному из четырех квадрантов на плоскости с координатами , тогда любая местность обитания на Земле может быть отнесена к одному из четырех квадрантов на плоскости с координатами 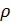 и и 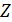 . Под координатой . Под координатой 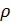 будем понимать плотность емкости среды обитания, а под координатой будем понимать плотность емкости среды обитания, а под координатой 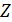 — высоту расположения над уровнем моря. На рис.10 приведено позиционирование каждого из четырех квадрантов с примерным сохранением масштабов по координатам. — высоту расположения над уровнем моря. На рис.10 приведено позиционирование каждого из четырех квадрантов с примерным сохранением масштабов по координатам.
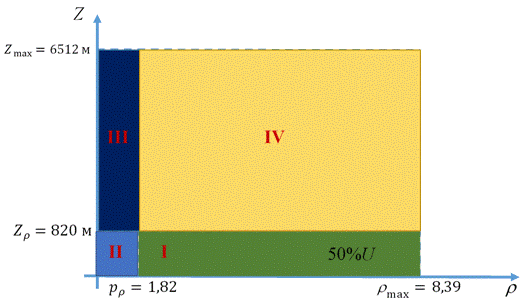
Рис.10. Позиционирование каждого из четырех квадрантов в пространстве с координатами 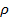 , , 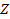
Согласно рис.10 квадрант I определяется парой условий: 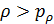 и и 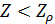 ; квадрант II — ; квадрант II — 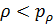 и и 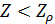 ; квадрант III — ; квадрант III — 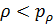 и и 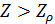 ; квадрант IV — ; квадрант IV — 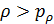 и и 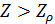 . В терминах “высоко – благоприятно”: первый квадрант наиболее благоприятен для жизни, т.е. эти территории расположены не очень высоко, и они благоприятны климатически; второй квадрант соответствует территориям, которые расположены не очень высоко, но они неблагоприятны с климатической точки зрения; третий квадрант отвечает наиболее суровым территориям, расположенным высоко и которые неблагоприятны с точки зрения климата, наконец, территории четвертого квадранта, хотя и расположены высоко, благоприятны с точки зрения климата. На рис.10 приведена также специфическая для каждого типа территорий окраска, используемая при построении карты на рис.12. . В терминах “высоко – благоприятно”: первый квадрант наиболее благоприятен для жизни, т.е. эти территории расположены не очень высоко, и они благоприятны климатически; второй квадрант соответствует территориям, которые расположены не очень высоко, но они неблагоприятны с климатической точки зрения; третий квадрант отвечает наиболее суровым территориям, расположенным высоко и которые неблагоприятны с точки зрения климата, наконец, территории четвертого квадранта, хотя и расположены высоко, благоприятны с точки зрения климата. На рис.10 приведена также специфическая для каждого типа территорий окраска, используемая при построении карты на рис.12.
На рис.11 приведены четыре карты территорий, соответствующих каждому из четырех квадратов рис.10. Территории в пределах отдельной категории окрашены на рис.11 случайными цветами. Исходные данные были взяты согласно расчетам предыдущего раздела. Итоги расчетов площадей территорий, объемов емкостей среды и количества территорий для каждого из квадрантов приведены в таблице №6.
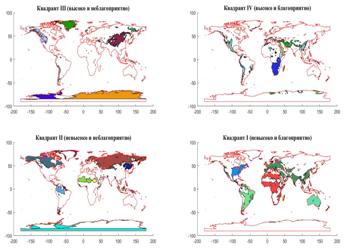
Рис.11. Карты территории с параметрами плотности емкости среды обитания и высоты позиционирования согласно четырем квадрантам
Площади территорий в таблице №6 приведены в единицах 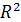 , где , где 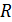 — радиус Земли. В частности, если в качестве единицы выбрать всю территорию первого квадранта, то отношение площадей всех четырех типов территорий составит 1: 0,59: 0,35: 0,30. Наконец, если в качестве единицы выбрать полную емкость среды обитания территорий первого квадранта, то отношение емкостей среды обитания всех четырех типов составит 1: 0,41: 0,21: 0,38. — радиус Земли. В частности, если в качестве единицы выбрать всю территорию первого квадранта, то отношение площадей всех четырех типов территорий составит 1: 0,59: 0,35: 0,30. Наконец, если в качестве единицы выбрать полную емкость среды обитания территорий первого квадранта, то отношение емкостей среды обитания всех четырех типов составит 1: 0,41: 0,21: 0,38.
|
Таблица №6. Набор площадей ( ), объемов емкостей среды обитания ( ), объемов емкостей среды обитания ( ) и числа территорий ( ) и числа территорий ( ) для каждого из квадрантов ) для каждого из квадрантов
|
|
Переменная
|
Квадрант I
|
Квадрант II
|
Квадрант III
|
Квадрант IV
|
Сумма
|
|
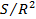
|
1,7909
|
1,0632
|
0,6276
|
0,5420
|
4,0237
|
|

|
3,8525
|
1,5796
|
0,8095
|
1,4623
|
7,7039
|
|
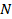
|
391
|
473
|
401
|
454
|
1719
|
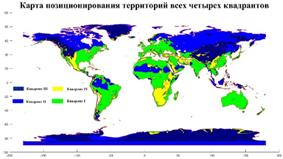
На рис.12,а приведена единая карта для территорий всех четырех качеств, при этом территории первого квадранта окрашены в зеленый цвет, территории второго квадранта — в синий, территории третьего квадранта — в фиолетовый и, наконец, территории четвертого — в желтый.
Рассмотрим более подробно карту, на которой изображена государственная граница РФ (на 2008 г.), а также территории, классифицируемые согласно рис.10. Результат приведен на рис.12,б. Из рис.12,б отчетливо видно, что практически вся территория РФ окрашена в синий цвет, т.к. она относится к категории “невысоко-неблагоприятно”. Небольшой фрагмент территорий первой категории “невысоко-благоприятно” (окрашены в зеленый цвет) расположен на западе страны.
Подсчитаем так называемый “индекс разнообразия территорий”, 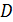 для всех стран и территорий, перечень которых рассмотрен ранее в разделе №3. Для этого определим понятие “индекс территории”, для всех стран и территорий, перечень которых рассмотрен ранее в разделе №3. Для этого определим понятие “индекс территории”, 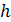 , который может принимать значения из набора (1; 0,41; 0,21; 0,38), введенного выше в связи со взаимной субординацией емкостей среды обитания четырех типов территорий. Определим индекс территории для каждой из точек сетки , который может принимать значения из набора (1; 0,41; 0,21; 0,38), введенного выше в связи со взаимной субординацией емкостей среды обитания четырех типов территорий. Определим индекс территории для каждой из точек сетки 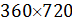 , тогда получим матрицу , тогда получим матрицу  , , 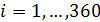 ; ; 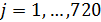 . В разделе №3 была рассмотрена база данных за 2008 г. 246 государств и территорий, для которых найдем индексы разнообразия территорий . В разделе №3 была рассмотрена база данных за 2008 г. 246 государств и территорий, для которых найдем индексы разнообразия территорий 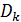 , ,  . .
|
|

|
|
Рис.12,а. Карта совместного позиционирование территорий всех четырех квадрантов
|
Рис.12,б. Карта территорий всех четырех качеств с разметкой государственной границы РФ (на 2008 г.)
|
Индекс разнообразия произвольной территории определим в виде дисперсии значений индекса территории, т.е.
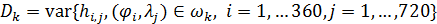 , (19) , (19)
где 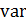 — операция нахождения дисперсии, — операция нахождения дисперсии, 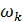 — область занимаемая на Земной сфере — область занимаемая на Земной сфере  -м государством или территорией, -м государством или территорией,  . .
Индекс разнообразия территорий (19) был подсчитан для всех 246 государств и территорий. На рис.13 приведен фрагмент итоговых данных для избранного набора государств. Если, для примера сравнить индексы разнообразия территорий США и РФ, то окажется это отношение равным 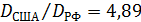 4. Таким образом, территория РФ приблизительно в пять раз менее разнообразна территории США. Это означает, что управление территорией США как целостностью более затратное, чем аналогичное управление территорией РФ. 4. Таким образом, территория РФ приблизительно в пять раз менее разнообразна территории США. Это означает, что управление территорией США как целостностью более затратное, чем аналогичное управление территорией РФ.
В итоге исследований, представленных в этом и предыдущем разделах, выяснилось следующее. Большинство народонаселения Земли стремится проживать на территориях, относимых к категории “невысоко – благоприятно” или, иначе, ближе к линии раздела “суша – океан”. Эта половина народонаселения наиболее мобильна в социальном плане, поскольку она ориентирована на океан, точнее, на океанский трафик. Другая, более консервативная часть населения, ориентирована на сушу и, соответственно, континентальный трафик. Эти соображения воспроизводят хорошо известное в геополитике (Х.Дж. Маккиндер, К. Хаусхоффер и ряд других авторов) противопоставление двух политических доктрин, условно названных “талассакратическая” и “теллурическая”, первая из которых ориентируется на приобретение политического могущества посредством океана, а вторая — посредством континента.
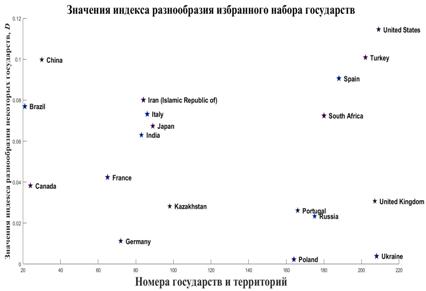
Рис.13. Значения индекса разнообразия территорий избранного набора государств
В данном разделе представлена нарезка территорий суши в терминах “(не)высоко – (не)благоприятно” (рис.12). Данная нарезка может быть рассмотрена в качестве предпосылки или рамок объяснения имеющейся конфигурации границ государств. Понятно, что в итоговом объяснении конфигурации государственных границ всегда присутствует изрядная доля предысторий становления того или иного государства (территории) в едином контексте мировой политической системы. Нас же в данном разделе интересовала унификация и классификация территорий в терминах климатических данных и рельефа.
Рассмотрим в дальнейшем иной способ нарезки территорий, в котором решающую роль играет трафик. Этот способ районирования должен органически учесть обе геополитические особенности (талассакратическая и теллурическая) управления территориями.
В начале разработаем алгоритм случайного распределения набора точек на поверхности суши с учетом плотности емкости среды обитания. В дальнейшем определим трафик между точками, затраты на трафик и соответственно определим задачу минимизации затрат на трафик путем оптимального перемещения точек, выступающих в качестве логистических узлов между территориями. Оптимальное положение набора узлов коммуникации плюс береговая линия определит искомые территориальные субъединицы — геопатомы.
6. Случайное распределение точек на поверхности Земли
Представим интеграл в (8) в виде суммы следующим образом. Определим в пределах среды обитания на поверхности Земли  точек с координатами точек с координатами  , , 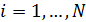 . Будем полагать, что все точки локализованы в пределах суши. Пусть каждой точке . Будем полагать, что все точки локализованы в пределах суши. Пусть каждой точке 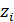 соответствует некоторая область соответствует некоторая область 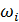 . В результате высказанных соображений глобальную емкость среды обитания (8) можно переписать в виде: . В результате высказанных соображений глобальную емкость среды обитания (8) можно переписать в виде:
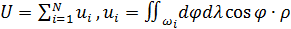 . (20) . (20)
Используя метод Монте-Карло разыграем процедуру случайного нанесения  точек в пределах суши. Разыгрывать потребуется двумерную случайную величину точек в пределах суши. Разыгрывать потребуется двумерную случайную величину 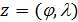 , содержащую компоненты широты и долготы. Учитывая предыдущие разделы, рассмотрим сетку значений широт и долгот с разрешением , содержащую компоненты широты и долготы. Учитывая предыдущие разделы, рассмотрим сетку значений широт и долгот с разрешением 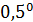 . В этом случае двумерная случайная величина . В этом случае двумерная случайная величина 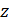 будет принимать набор значений будет принимать набор значений  , , 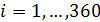 ; ; 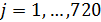 . Матрицу распределения . Матрицу распределения 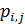 случайной величины случайной величины 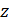 запишем в виде: запишем в виде:
 , (21) , (21)
где 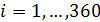 ; ; 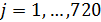 . .
Если просуммировать матрицу (21) по строкам и столбцам, найдем ряды распределения по широте, 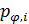 и долготе, и долготе, 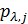 , т.е. , т.е.
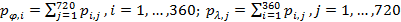 . (22) . (22)

Рис.14. Ряды распределения компонент широты (левый график) и долготы (правый график) случайного двумерного вектора z
Построим ряды распределений (22). Для этого подставим в (21) плотность емкости среды согласно формуле (3) с параметрами из пункта №5 таблицы №1. Результат приведен на рис.14.
Изучение левого графика на рис.14 подтверждает ожидания о том, что вероятность к полюсам должна понижаться при случайном разыгрывании компоненты широты случайного вектора 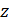 . С учетом вида плотности емкости среды (3) понятно, что компоненты случайного вектора . С учетом вида плотности емкости среды (3) понятно, что компоненты случайного вектора 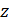 не являются независимыми. По этой причине для разыгрывания каждой из компонент необходимо знать одну из двух условных матриц вероятностей вида: не являются независимыми. По этой причине для разыгрывания каждой из компонент необходимо знать одну из двух условных матриц вероятностей вида:
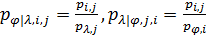 , (23) , (23)
где 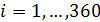 ; ; 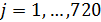 . .
Рассмотрим процедуру разыгрывания каждой из компонент вектора 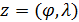 в отдельности. С учетом (22) случайные величины в отдельности. С учетом (22) случайные величины 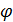 и и 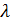 принимают значения принимают значения 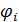 и и 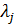 с вероятностями с вероятностями 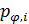 и и 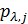 , где , где 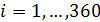 ; ; 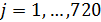 . Составим кумулятивные наборы вероятностей следующего вида: . Составим кумулятивные наборы вероятностей следующего вида:
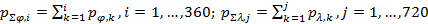 . (24) . (24)
С учетом (24) разыгрывание любой из двух случайных дискретных величин 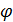 , , 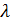 сводится к следующей процедуре. Для определенности выберем широту, для долготы процедура аналогична. Генерируем равномерно распределенное на отрезке [0;1] случайное число сводится к следующей процедуре. Для определенности выберем широту, для долготы процедура аналогична. Генерируем равномерно распределенное на отрезке [0;1] случайное число 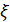 ; находим номер интервала из набора ; находим номер интервала из набора  , , 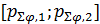 , …, , …, 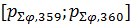 , в который попадает случайное число , в который попадает случайное число 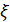 . Обозначим полученный номер выражением . Обозначим полученный номер выражением  , тогда разыгранное значение случайной величины , тогда разыгранное значение случайной величины 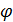 составит составит 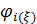 . .
Вернемся к разыгрыванию двумерной случайной величины 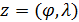 . Пусть, например, разыграна широта и получено значение . Пусть, например, разыграна широта и получено значение 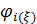 . Надо разыграть долготу при известной широте . Надо разыграть долготу при известной широте 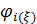 , т.е. необходимо воспользоваться условной вероятностью , т.е. необходимо воспользоваться условной вероятностью 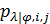 из (23), когда из (23), когда 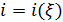 . Другими словами, задача сводится к разыгрыванию условной дискретной случайной величины . Другими словами, задача сводится к разыгрыванию условной дискретной случайной величины 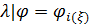 , принимающей значения , принимающей значения 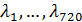 с вероятностями с вероятностями 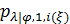 , …, , …, 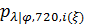 . Применим процедуру, аналогичную при разыгрывании широты, т.е. найдем соответствующие кумулятивные наборы, сгенерируем равномерно распределенное на отрезке [0;1] случайное число . Применим процедуру, аналогичную при разыгрывании широты, т.е. найдем соответствующие кумулятивные наборы, сгенерируем равномерно распределенное на отрезке [0;1] случайное число 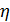 и определим номер интервала и определим номер интервала 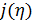 , в который попадает случайное число , в который попадает случайное число 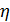 . .
В итоге изложенного выше алгоритма, завершается процедура разыгрывания двумерной случайной величины 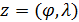 , т.е. находится пара , т.е. находится пара 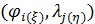 , генерация которых может быть продолжена без ограничений. В конкретных расчетах алгоритм был несколько иной. Пусть генерируется , генерация которых может быть продолжена без ограничений. В конкретных расчетах алгоритм был несколько иной. Пусть генерируется  пар значений пар значений 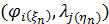 , , 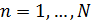 . Для четных значений . Для четных значений 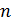 разыгрывалась вначале широта, а затем с помощью условной вероятности разыгрывалась долгота и, наоборот, при нечетном разыгрывалась вначале широта, а затем с помощью условной вероятности разыгрывалась долгота и, наоборот, при нечетном 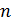 разыгрывалась вначале долгота, а затем с помощью условной вероятности разыгрывалась широта. разыгрывалась вначале долгота, а затем с помощью условной вероятности разыгрывалась широта.
На рис.15 приведен итог применения, изложенного выше алгоритма в виде одной из версий случайного нанесения 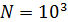 точек в пределах суши с учетом плотности емкости среды обитания. точек в пределах суши с учетом плотности емкости среды обитания.

Рис.15. Случайное распределение 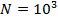 точек с учетом плотности емкости среды обитания точек с учетом плотности емкости среды обитания
7. Трафик между территориями
Учтем наличие корреспонденций или трафика между парой территорий с номерами 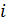 и и 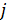 ( (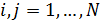 ). В предыдущем разделе был разработан алгоритм случайного распределения ). В предыдущем разделе был разработан алгоритм случайного распределения  точек на поверхности Земли с учетом плотности емкости среды обитания. С каждой из точек свяжем определенную территорию, которая будет обладать соответствующей емкостью среды обитания точек на поверхности Земли с учетом плотности емкости среды обитания. С каждой из точек свяжем определенную территорию, которая будет обладать соответствующей емкостью среды обитания 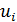 , , 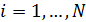 . В качестве таких территорий возьмем многоугольники Вороного для конечного набора точек . В качестве таких территорий возьмем многоугольники Вороного для конечного набора точек  , ,  на поверхности Земли. Набор на поверхности Земли. Набор  точек можно истолковать в том числе и в качестве логистических узлов по транспортировке части емкости среды обитания между территориями. точек можно истолковать в том числе и в качестве логистических узлов по транспортировке части емкости среды обитания между территориями.
На рис.16 приведен пример распределения методом Монте-Карло  точек на поверхности Земли с учетом процедуры (21) — (24). Там же с учетом береговой линии и полюсов нанесены соответствующие многоугольники Вороного. При построении многоугольников Вороного в координатах “широта – долгота” имела место особенность, связанная с полюсами. Вводились дополнительно четыре “фиктивные” точки: точек на поверхности Земли с учетом процедуры (21) — (24). Там же с учетом береговой линии и полюсов нанесены соответствующие многоугольники Вороного. При построении многоугольников Вороного в координатах “широта – долгота” имела место особенность, связанная с полюсами. Вводились дополнительно четыре “фиктивные” точки:  , ,  , , 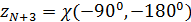 , , 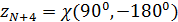 , где , где 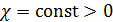 . В расчетах параметр . В расчетах параметр  выбирался, равным 5. Далее находились многоугольники Вороного по расширенному набору точек выбирался, равным 5. Далее находились многоугольники Вороного по расширенному набору точек  , ,  . В рамках данной процедуры гарантировано конечные многоугольники Вороного включали береговую линию, а неограниченные многоугольники были вынесены в фиктивную область. . В рамках данной процедуры гарантировано конечные многоугольники Вороного включали береговую линию, а неограниченные многоугольники были вынесены в фиктивную область.
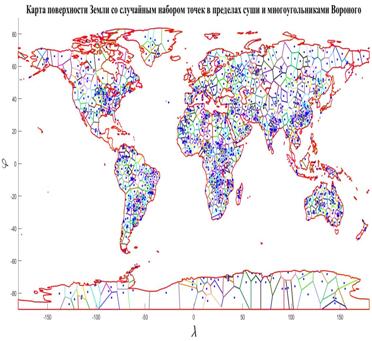
Рис.16. Карта поверхности Земли со случайным набором точек в пределах суши и многоугольниками Вороного
В начале определим трафик, сопровождение которого беззатратно. Определим матрицу  , , 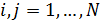 , элементы которой характеризуют передачу доли , элементы которой характеризуют передачу доли 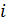 -й емкости среды обитания в -й емкости среды обитания в 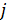 -ю емкость среды обитания в связи с трафиком. Матрица -ю емкость среды обитания в связи с трафиком. Матрица  , , 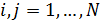 выступает в качестве меры обмены емкостью среды обитания между набором точек выступает в качестве меры обмены емкостью среды обитания между набором точек  , , 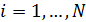 на поверхности Земли. Согласно определению следует, что на поверхности Земли. Согласно определению следует, что
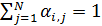 , (25) , (25)
где 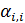 — доля — доля 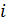 -й емкости среды обитания не подверженная трафику, т.е. это та доля, которая остается внутри -й емкости среды обитания не подверженная трафику, т.е. это та доля, которая остается внутри 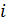 -й территории. Набор емкостей среды обитания -й территории. Набор емкостей среды обитания 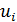 , , 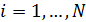 выступает в качестве некоторого ресурса, который в контексте трафика считается универсальным и аддитивным. выступает в качестве некоторого ресурса, который в контексте трафика считается универсальным и аддитивным.
Найдем количество емкости среды обитания,  покинувшее вследствие трафика покинувшее вследствие трафика 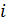 -ю территорию и соответствующее количество емкости среды обитания, -ю территорию и соответствующее количество емкости среды обитания, 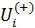 прибывшее в прибывшее в 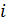 -ю территорию, тогда -ю территорию, тогда
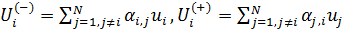 . (26) . (26)
Принимая во внимание (25), непосредственной проверкой можно установить, что имеет место баланс прихода и ухода емкости среды обитания, 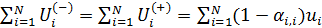 , т.е. вследствие беззатратного трафика сколько уходит столько и приходит. , т.е. вследствие беззатратного трафика сколько уходит столько и приходит.
Пусть теперь при перемещении части емкости среды обитания из пункта 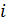 в пункт в пункт 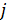 доля ресурса доля ресурса 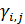 вследствие трафика теряется, считаем при этом, что вследствие трафика теряется, считаем при этом, что 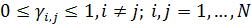 . Полагаем, что в пределах логистического пункта затраты отсутствуют, т.е. . Полагаем, что в пределах логистического пункта затраты отсутствуют, т.е. 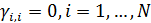 . Матрицу . Матрицу 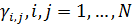 назовем матрицей затрат на транспорт. С учетом (26) составим функционал, назовем матрицей затрат на транспорт. С учетом (26) составим функционал, 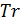 всех транспортных затрат: всех транспортных затрат:
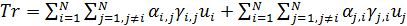 . (27) . (27)
Смысл транспортного функционала (27) прозрачен: при перемещении ресурса из пункта 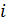 в пункт в пункт 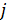 часть его в количестве часть его в количестве 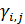 расходуется, аналогично при перемещении ресурса из пункта расходуется, аналогично при перемещении ресурса из пункта 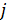 в пункт в пункт 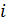 часть ресурса в количестве часть ресурса в количестве 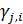 также расходуется. Транспортный функционал (27) можно несколько упростить, учитывая, что первая и вторая двойные суммы совпадают, это видно после переобозначения индексов, т.е. также расходуется. Транспортный функционал (27) можно несколько упростить, учитывая, что первая и вторая двойные суммы совпадают, это видно после переобозначения индексов, т.е.
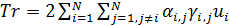 . . 
В связи с формулой 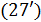 можно поставить оптимизационную задачу о минимизации затрат на корреспонденции можно поставить оптимизационную задачу о минимизации затрат на корреспонденции 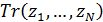 путем подходящего смещения точек путем подходящего смещения точек 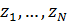 в пределах суши. Понятно, что в качестве глобального минимума затрат на транспорт выступает нулевое значение, когда в пределах суши. Понятно, что в качестве глобального минимума затрат на транспорт выступает нулевое значение, когда  . В математическом виде задача минимизации сводится к поиску набора точек . В математическом виде задача минимизации сводится к поиску набора точек 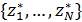 , который, быть может не единственен, при котором реализуется один из локальных минимумов издержек на трафик, т.е. , который, быть может не единственен, при котором реализуется один из локальных минимумов издержек на трафик, т.е.
 . (28) . (28)
Для дальнейшего продвижения в решении задачи оптимизации (28) необходимы дополнительные уточнения вида матриц  . Привлечем к рассмотрению хорошо известную в теории транспортных потоков так называемую гравитационную модель [8,9], в которой вводится некоторое обобщенное “расстояние” . Привлечем к рассмотрению хорошо известную в теории транспортных потоков так называемую гравитационную модель [8,9], в которой вводится некоторое обобщенное “расстояние” 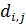 ( (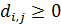 ) между ) между 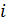 -й и -й и 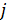 -й территориями. Отметим, что матрица расстояний -й территориями. Отметим, что матрица расстояний 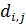 , , 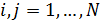 , вообще говоря, не является симметричной, т.е. , вообще говоря, не является симметричной, т.е. 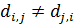 , тогда как по определению считается, что , тогда как по определению считается, что 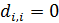 , , 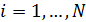 . Отметим, что из условия . Отметим, что из условия 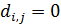 не обязательно следует, что точки не обязательно следует, что точки 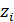 и и 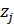 совпадают в физическом пространстве. совпадают в физическом пространстве.
Выберем экспоненциальную зависимость коэффициентов матрицы  , , 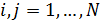 от расстояния, тогда можно записать следующее представление: от расстояния, тогда можно записать следующее представление:
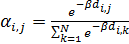 , (29) , (29)
где 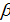 — некоторый неотрицательный параметр. Непосредственной проверкой можно убедиться в выполнении для матрицы — некоторый неотрицательный параметр. Непосредственной проверкой можно убедиться в выполнении для матрицы  , , 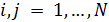 в форме (29) условия (25). в форме (29) условия (25).
Следуя экспоненциальной зависимости матрицы  , , 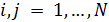 от расстояния в (29), выберем следующее простейшее представление для матрицы затрат на транспорт: от расстояния в (29), выберем следующее простейшее представление для матрицы затрат на транспорт:
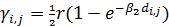 , (30) , (30)
где 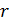 и и 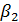 — некоторые постоянные неотрицательные коэффициенты. Согласно (30) при — некоторые постоянные неотрицательные коэффициенты. Согласно (30) при 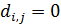 затраты на транспорт отсутствуют, т.е. затраты на транспорт отсутствуют, т.е.  . Наконец, при . Наконец, при 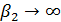 и при и при 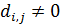 следует, что следует, что 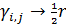 , т.е. доля затрат на транспорт становится постоянной величиной, равной , т.е. доля затрат на транспорт становится постоянной величиной, равной 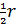 . Из последнего замечания следует, что . Из последнего замечания следует, что  . .
Подставим (29), (30) в 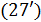 , тогда найдем следующее выражение для суммарных затрат на транспорт: , тогда найдем следующее выражение для суммарных затрат на транспорт:
 . . 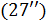
Для транспортных затрат в форме 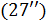 характерны следующие свойства, проверяемые непосредственно. Во-первых, когда расстояние между точками становится нулевым, т.е. характерны следующие свойства, проверяемые непосредственно. Во-первых, когда расстояние между точками становится нулевым, т.е. 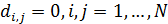 , затраты на транспорт отсутствуют, , затраты на транспорт отсутствуют,  . Во-вторых, когда расстояние между точками стремится к бесконечности, т.е. . Во-вторых, когда расстояние между точками стремится к бесконечности, т.е. 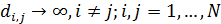 , затраты на транспорт в силу выбранных зависимостей (29), (30) также стремятся к нулю, , затраты на транспорт в силу выбранных зависимостей (29), (30) также стремятся к нулю, 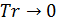 . Отметим, что расстояние, равное нулю, либо стремящееся к бесконечности между парой точек, не означает, что точки сливаются или расходятся на бесконечность. . Отметим, что расстояние, равное нулю, либо стремящееся к бесконечности между парой точек, не означает, что точки сливаются или расходятся на бесконечность.
Рассмотрим транспортные затраты в форме 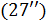 как функцию параметра как функцию параметра 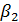 , т.е. , т.е. 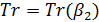 . В этом случае очевидно, что . В этом случае очевидно, что 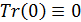 . Пусть теперь . Пусть теперь 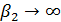 , тогда , тогда 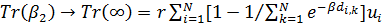 . Для последнего функционала транспортных затрат очевидно, что глобальный минимум, равный нулю, достигается только в том случае, когда расстояния между точками стремятся к бесконечности. Именно последний вариант функционала будет рассмотрен в дальнейшем с точки зрения вычислительного эксперимента. В этом случае точки не смогут собраться вместе, они будут отталкиваться и заполнят максимум среды обитания, т.к. “заперты” на поверхности земной сферы. . Для последнего функционала транспортных затрат очевидно, что глобальный минимум, равный нулю, достигается только в том случае, когда расстояния между точками стремятся к бесконечности. Именно последний вариант функционала будет рассмотрен в дальнейшем с точки зрения вычислительного эксперимента. В этом случае точки не смогут собраться вместе, они будут отталкиваться и заполнят максимум среды обитания, т.к. “заперты” на поверхности земной сферы.
Условие предельного перехода 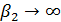 назовем “минимаксной транспортной доктриной”, которая расшифровывается согласно формуле: минимум транспортных издержек при максимуме заполнения емкости среды обитания. назовем “минимаксной транспортной доктриной”, которая расшифровывается согласно формуле: минимум транспортных издержек при максимуме заполнения емкости среды обитания.
Подставим 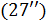 в (28), тогда в общем случае задача минимизации транспортных издержек перепишется в виде: в (28), тогда в общем случае задача минимизации транспортных издержек перепишется в виде:
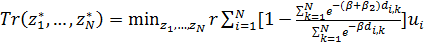 . (31) . (31)
Уточним задачу минимизации (31) в упрощенном виде, когда считается, что 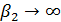 , т.е. имеет место минимаксная транспортная доктрина минимума транспортных издержек при максимуме заполнения емкости среды обитания, тогда , т.е. имеет место минимаксная транспортная доктрина минимума транспортных издержек при максимуме заполнения емкости среды обитания, тогда
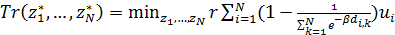 . . 
Для определения алгоритма подсчета матрицы расстояний 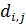 , , 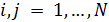 выскажем ряд физических соображений об энергетических затратах по перемещению одной условной единицы веса груза из пункта выскажем ряд физических соображений об энергетических затратах по перемещению одной условной единицы веса груза из пункта 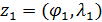 в пункт в пункт 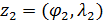 . Пусть определен маршрут перемещения груза в виде линии: . Пусть определен маршрут перемещения груза в виде линии: 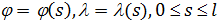 . В качестве аргумента параметризации линии выступает длина линии, . В качестве аргумента параметризации линии выступает длина линии,  , изменяющаяся от нуля до своего максимального значения, , изменяющаяся от нуля до своего максимального значения, 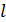 , равного длине маршрута, при этом считается, что , равного длине маршрута, при этом считается, что 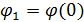 , , 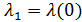 и и 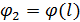 , , 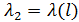 . .
Пусть в начале маршрут движения полностью расположен на поверхности суши. В этом случае энергетика затрат на перемещение одной условной единицы веса груза складывается из трех характерных вариантов движений: 1) вертикальное перемещение груза вверх в связи особенностями рельефа; 2) вертикальное опускание груза в связи с особенностями рельефа; 3) перемещение груза по наклонной поверхности. Первые два пункта вариантов движения описывают энергетические затраты по перемещению груза “вверх – вниз”. Последний пункт характеризуется, главным образом, энергетическими затратами на преодоление трения качения в рамках таких видов транспорта, как автомобильный и железнодорожный. Пусть 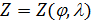 — рельеф поверхности суши, тогда для выбранного маршрута перемещения условной единицы массы груза можно записать функцию — рельеф поверхности суши, тогда для выбранного маршрута перемещения условной единицы массы груза можно записать функцию 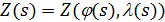 , , 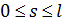 . .
С учетом высказанных физических соображений запишем формулу для подсчета расстояния по выбранной траектории между парой пунктов 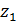 и и 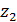 , , 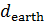 : :
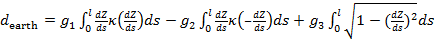 , (32) , (32)
где 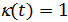 , , 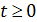 ; ;  , , 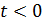 — так называемая “единичная” функция. Неизвестные неотрицательные параметры — так называемая “единичная” функция. Неизвестные неотрицательные параметры 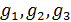 характеризуют вклад каждого из видов движений по перемещению одной условной единицы массы груза. Интегралы, входящие в (32) назовем транспортными интегралами. характеризуют вклад каждого из видов движений по перемещению одной условной единицы массы груза. Интегралы, входящие в (32) назовем транспортными интегралами.
Пусть теперь маршрут движения одной условной единицы массы груза лежит полностью в море, т.е. и пункты отправки, прибытия, и все прочие точки маршрута лежат на поверхности моря. В этом случае энергетические затраты по перемещению одной единицы веса условного груза морским транспортом связаны с преодолением вязкого трения. Для подсчета расстояния по выбранной траектории между парой пунктов 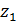 и и 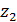 , , 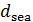 можно воспользоваться формулой (32). Считаем, что водный транспорт движется по горизонтальной поверхности, для которой можно считать, что можно воспользоваться формулой (32). Считаем, что водный транспорт движется по горизонтальной поверхности, для которой можно считать, что 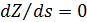 . Учитывая последней интеграл в (32) и производя элементарное интегрирование, запишем соответствующий транспортный интеграл в виде: . Учитывая последней интеграл в (32) и производя элементарное интегрирование, запишем соответствующий транспортный интеграл в виде:
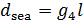 , (33) , (33)
где 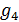 — некоторый неотрицательный параметр, учитывающий усредненные особенности вязкого трения в водной среде совокупного водного транспорта. — некоторый неотрицательный параметр, учитывающий усредненные особенности вязкого трения в водной среде совокупного водного транспорта.
Отметим, что произвольный маршрут между пунктом отправления и назначения можно разбить на этапы движения только по суше или только по морю. Применяя к каждому этапу либо формулу (32), либо формулу (33) и складывая полученные значения, найдем итоговое расстояние между парой пунктов. Расстояния, подсчитанные по формулам (32), (33), не являются расстояниями в обычном смысле слова. Они скорее выступают в качестве эффективных расстояний, которые всегда можно измерить, подсчитав среднюю энергию по перемещению одной условной единицы массы груза из пункта отправки в пункт назначения.
Исходя из физических соображений, оценим по порядку величины параметры 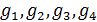 . При подъеме груза по наклонной плоскости работа в части подъема выражается формулой: . При подъеме груза по наклонной плоскости работа в части подъема выражается формулой: 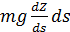 , где m — масс груза, а , где m — масс груза, а  — ускорение свободного падения. Найдем удельную работу на единицу веса груза путем деления на — ускорение свободного падения. Найдем удельную работу на единицу веса груза путем деления на  , она равна , она равна  , т.е. , т.е. 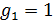 . .
Несколько иная ситуация складывается при движении груза по наклонной плоскости в случае спуска. Не совсем понятно сколько в среднем энергии обычному наземному транспорту (автомобильному и железнодорожному) требуется при спуске. Самый простой случай, считать, что требуется столько же энергии, сколько и при подъеме, тогда найдем 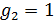 . .
Для оценки третьего параметра необходимо учесть формулу для определения трения качения. Пусть 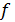 — трение качения, а — трение качения, а 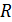 — радиус колеса, тогда можно записать следующую формулу для работы по преодолению силы качения: — радиус колеса, тогда можно записать следующую формулу для работы по преодолению силы качения:  . Отметим, что трение качения резины по асфальту для автотранспорта, . Отметим, что трение качения резины по асфальту для автотранспорта,  и трение качения стали по стали для железнодорожного транспорта, и трение качения стали по стали для железнодорожного транспорта, 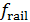 можно считать равными по порядку величины, т.е. можно считать равными по порядку величины, т.е. 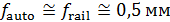 . Считаем, что средний радиус колеса совокупного автомобиля и вагона железнодорожного транспорта порядка 0,5 м. В этом случае удельная работа по перемещению единицы веса груза составит . Считаем, что средний радиус колеса совокупного автомобиля и вагона железнодорожного транспорта порядка 0,5 м. В этом случае удельная работа по перемещению единицы веса груза составит  . Подставляя . Подставляя 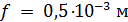 и и  , найдем , найдем 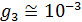 . .
Перейдем к оценке численного коэффициента 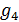 . Для этого рассчитаем силу сопротивления . Для этого рассчитаем силу сопротивления 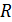 для типичного контейнеровоза [10] с габаритами: длина, для типичного контейнеровоза [10] с габаритами: длина, 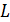 = 157 м; ширина, = 157 м; ширина, 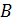 = 25,4 м; осадка, = 25,4 м; осадка, 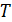 = 9,22 м, водоизмещение, = 9,22 м, водоизмещение, 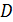 = 22800 т; расчетная скорость, = 22800 т; расчетная скорость, 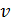 = 19 узлов = 9,77 м/сек. Для подсчета силы трения сопротивления принято использовать формулу = 19 узлов = 9,77 м/сек. Для подсчета силы трения сопротивления принято использовать формулу  , где , где 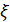 — сложный агрегированный коэффициент сопротивления трения, — сложный агрегированный коэффициент сопротивления трения, 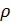 — плотность морской воды, — плотность морской воды, 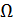 — смоченная поверхность корпуса корабля. Поделим силу сопротивления на вес судна, равный — смоченная поверхность корпуса корабля. Поделим силу сопротивления на вес судна, равный 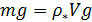 , , 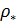 — средняя плотность массы корабля с грузом, — средняя плотность массы корабля с грузом, 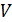 — объем судна, приближенно его водоизмещение, — объем судна, приближенно его водоизмещение,  — ускорение свободного падения. В итоге можно записать следующую оценку для искомого коэффициента: — ускорение свободного падения. В итоге можно записать следующую оценку для искомого коэффициента: 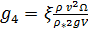 . Считаем, что . Считаем, что 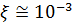 , , 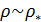 . Величину смоченной поверхности вычислим по формуле Мурагина . Величину смоченной поверхности вычислим по формуле Мурагина 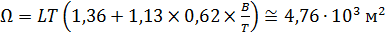 . В итоге надем . В итоге надем  . Отметим, что в рамках нашего анализа по порядку величины удельные энергетические затраты на перемещение единицы массы груза с помощью наземного и водного транспортов совпадают. . Отметим, что в рамках нашего анализа по порядку величины удельные энергетические затраты на перемещение единицы массы груза с помощью наземного и водного транспортов совпадают.
В задаче оптимизации 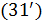 набор емкостей среды обитания отдельных регионов набор емкостей среды обитания отдельных регионов 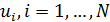 считался фиксированным. Однако это не отвечает процедуре нарезки территорий с помощью многоугольников Вороного. Действительно, по мере оптимизации расположения точек считался фиксированным. Однако это не отвечает процедуре нарезки территорий с помощью многоугольников Вороного. Действительно, по мере оптимизации расположения точек 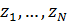 , их положения будут меняться, что приведет к изменению расположения соответствующих многоугольников Вороного. По этой причине в , их положения будут меняться, что приведет к изменению расположения соответствующих многоугольников Вороного. По этой причине в 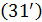 необходимо иметь в виду набор необходимо иметь в виду набор 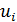 , i = 1,…,N, полученный в связи с текущим набором точек , i = 1,…,N, полученный в связи с текущим набором точек 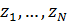 и тем, что и тем, что 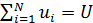 , где , где  — емкость среды обитания в пределах суши, — емкость среды обитания в пределах суши, 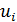 — емкость среды обитания многоугольника Вороного — емкость среды обитания многоугольника Вороного 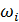 . В итоге задачу оптимизации . В итоге задачу оптимизации 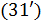 следует переписать в виде: следует переписать в виде:
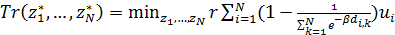 , (34) , (34)
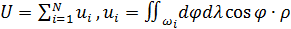 . (35) . (35)
Для решения задачи оптимизации (34), (35) будем применять метод простой итерации, выбирая набор 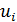 , i = 1,…,N в (34) с предыдущей итерации. Поиск минимума в (34) позволяет найти набор точек , i = 1,…,N в (34) с предыдущей итерации. Поиск минимума в (34) позволяет найти набор точек 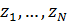 на следущей итерации, по которым определяем новый набор на следущей итерации, по которым определяем новый набор 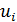 , , 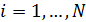 и так далее. Пусть и так далее. Пусть 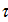 — номер итерации, — номер итерации, 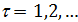 , тогда задача (34), (35) может быть переписана в виде: , тогда задача (34), (35) может быть переписана в виде:
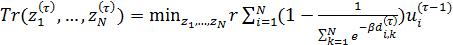 , , 
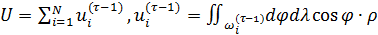 . . 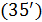
Задача оптимизации  , , 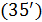 решается итеративно до тех пор, пока последовательности решается итеративно до тех пор, пока последовательности 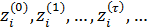 не сойдутся для каждого не сойдутся для каждого 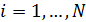 , при этом считается, что набор , при этом считается, что набор 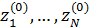 определяет начальное расположение точек, а набор определяет начальное расположение точек, а набор 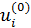 , , 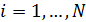 соответствующий перечень емкостей среды обитания многоугольников Вороного. соответствующий перечень емкостей среды обитания многоугольников Вороного.
8. Методика расчета матрицы расстояний
Для подсчета обобщенного расстояния (32), (33) между произвольной парой точек на поверхности Земли 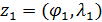 , , 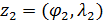 построим в начале траекторию малого фрагмента полной окружности Земли, проходящей через заданную пару точек. Считаем, что полная окружность лежит в плоскости, проходящей через центр Земли. Другими словами, построим линию: построим в начале траекторию малого фрагмента полной окружности Земли, проходящей через заданную пару точек. Считаем, что полная окружность лежит в плоскости, проходящей через центр Земли. Другими словами, построим линию: 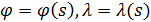 , где , где  — параметр, описывающим длину фрагмента окружности. Считаем, что — параметр, описывающим длину фрагмента окружности. Считаем, что 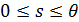 , , 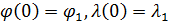 и и 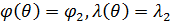 , где , где 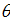 — длина дуги фрагмента полной окружности Земли. — длина дуги фрагмента полной окружности Земли.
Определим два единичных по длине вектора 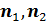 , которые указывают на пару выбранных точек , которые указывают на пару выбранных точек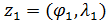 , , 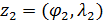 , тогда , тогда
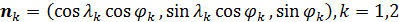 . (36) . (36)
Пусть вектор 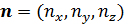 единичной длины указывает на произвольную точку полной окружности, проходящей через выбранную пару точек. Понятно, что вектор единичной длины указывает на произвольную точку полной окружности, проходящей через выбранную пару точек. Понятно, что вектор  лежит в плоскости, образованной векторами лежит в плоскости, образованной векторами 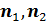 . Учитывая (36), после несложных преобразований, найдем . Учитывая (36), после несложных преобразований, найдем
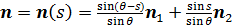 , (37) , (37)
где 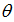 — угол между парой векторов — угол между парой векторов 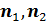 . Согласно (37) очевидно, что . Согласно (37) очевидно, что  и и 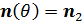 . .
Учитывая (37), а также считая, что 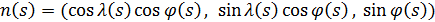 , найдем параметрическую запись полной окружности в координатах “широта – долгота”: , найдем параметрическую запись полной окружности в координатах “широта – долгота”:
 , (38) , (38)
 . . 
Отметим, что формула  верна, когда верна, когда 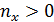 . В двух других случаях: 1) . В двух других случаях: 1) 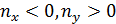 ; 2) ; 2)  к выражению в (38¢) необходимо добавить и вычесть p соответственно. к выражению в (38¢) необходимо добавить и вычесть p соответственно.
При проведении линии между парой точек согласно формулам (38),  необходимо также найти ее пересечение с береговой линией для выделения тех частей траектории, которые лежат отдельно на суше и на море. Для изображения траекторий (38), необходимо также найти ее пересечение с береговой линией для выделения тех частей траектории, которые лежат отдельно на суше и на море. Для изображения траекторий (38),  необходимо различать два случай: 1) необходимо различать два случай: 1)  ; 2) ; 2)  . В первом случае нулевой меридиан поместим в центр карты, т.е. в центре будет располагаться Атлантический океан. Во втором случае после сдвига долготы . В первом случае нулевой меридиан поместим в центр карты, т.е. в центре будет располагаться Атлантический океан. Во втором случае после сдвига долготы  построим карту с центром по линии смены дат, т.е. с центром в Тихом океане. построим карту с центром по линии смены дат, т.е. с центром в Тихом океане.
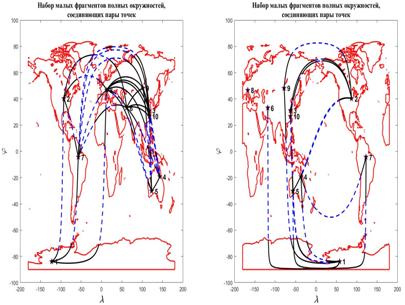
Рис.17. Набор малых фрагментов полных окружностей, соединяющих пары точек
На рис.17 приведен пример позиционирования десяти точек на поверхности суши. Точки выбраны случайно согласно алгоритму раздела №6, т.е. с учетом плотности емкости среды обитания. Точки пронумерованы и изображены на каждой из двух карт. На рис.17 с учетом сферической геометрии построены также все 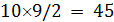 линий, соединяющих каждую пару точек. Кроме того, линии размечены в части их прохождения по суше (сплошная линия), и по морю (пунктирная линия). Согласно рис.17 некоторая часть бинарных линий позиционирована на правой карте с центром в Тихом океане. линий, соединяющих каждую пару точек. Кроме того, линии размечены в части их прохождения по суше (сплошная линия), и по морю (пунктирная линия). Согласно рис.17 некоторая часть бинарных линий позиционирована на правой карте с центром в Тихом океане.
Согласно формуле (32) для подсчета эффективного расстояния по перемещению одной условной единицы массы груза на поверхности Земли важно знать производную рельефа 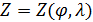 по маршруту, который опишем некоторой траекторией. Пусть, например, между парой точек по маршруту, который опишем некоторой траекторией. Пусть, например, между парой точек 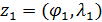 , , 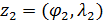 проложен маршрут такой, что проложен маршрут такой, что 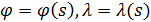 , где , где  — параметр, описывающий пройденный путь от начальной точки. В этом случае очевидно, что — параметр, описывающий пройденный путь от начальной точки. В этом случае очевидно, что 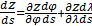 . .
В качестве маршрута между парой точек на поверхности Земной сферы выберем меньший фрагмент полной окружности, проходящей через пару точек. Подходящая траектория представлена в виде формул (38),  . Осталось найти производные. После несложных выкладок получим: . Осталось найти производные. После несложных выкладок получим:
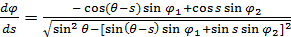 , (39) , (39)
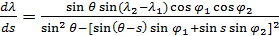 . . 
Опишем большой фрагмент полной окружности, проходящей через некоторую пару точек на поверхности Земли. С учетом описания малого фрагмента полной окружности (37), (38), 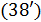 , параметризацию большого фрагмента целесообразно произвести в два этапа: 1) для значений параметра длины дуги , параметризацию большого фрагмента целесообразно произвести в два этапа: 1) для значений параметра длины дуги  из диапазона из диапазона  , где , где  ; 2) для значений параметра длины дуги ; 2) для значений параметра длины дуги  из диапазона из диапазона 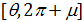 . Угол . Угол  найдем из условия того, что долгота найдем из условия того, что долгота  совпадает с меридианом смены дат, т.е. совпадает с меридианом смены дат, т.е. 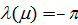 . Из решения последнего уравнения найдем . Из решения последнего уравнения найдем  , когда , когда 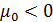 и и 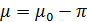 , когда , когда 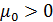 , при этом , при этом
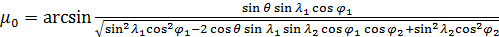 . .
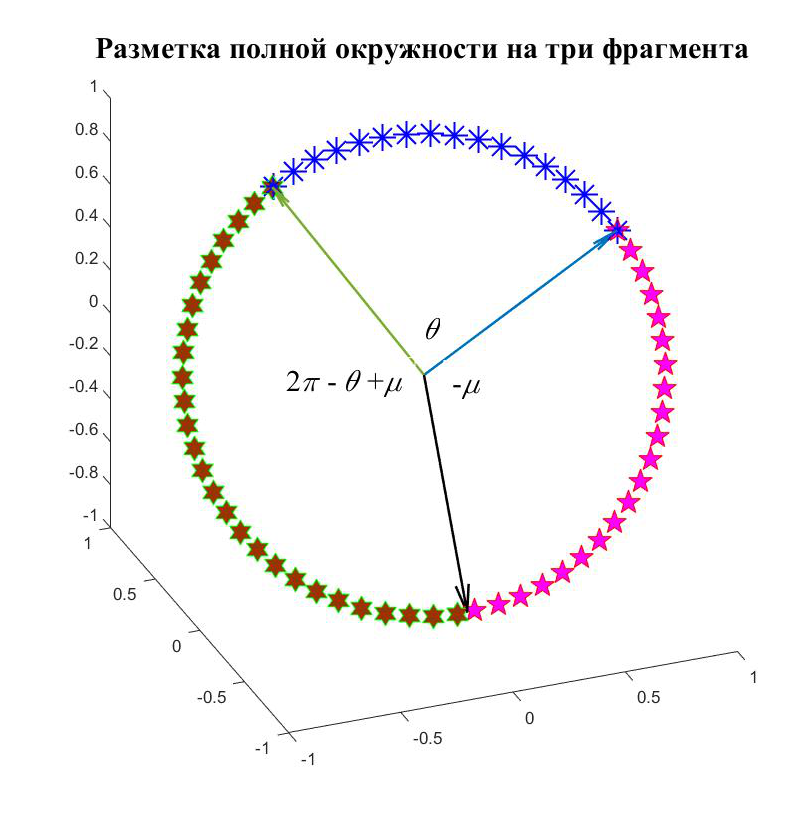
Рис.18. Разметка полной окружности на три фрагмента
На рис.18 приведен пример полной окружности, проходящей через пару случайно выбранных точек на поверхности Земли. Окружность поделена на три дуги: 1) малый фрагмент полной окружности помечен маркерами в виде звезд; 2) большой фрагмент полной окружности, параметризованный отрезком дуги  из диапазона из диапазона 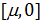 , где , где 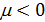 , помечен пентаграммами; 3) большой фрагмент полной окружности, параметризованный отрезком дуги , помечен пентаграммами; 3) большой фрагмент полной окружности, параметризованный отрезком дуги  из диапазона из диапазона 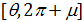 и помечен гексаграммами. Каждая из дуг отмечена соответствующим углом. Стрелка, отделяющая пентаграммы и гексаграммы, обозначает линию смены дат. После объединения второго и третьего фрагментов дуг получим большой фрагмент полной окружности. и помечен гексаграммами. Каждая из дуг отмечена соответствующим углом. Стрелка, отделяющая пентаграммы и гексаграммы, обозначает линию смены дат. После объединения второго и третьего фрагментов дуг получим большой фрагмент полной окружности.
Введем матрицу расстояний 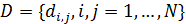 между всеми парами точек. Определим подобные матрицы расстояний, найденные для малых между всеми парами точек. Определим подобные матрицы расстояний, найденные для малых  и больших и больших  фрагментов дуг соответствующих полных окружностей. Учитывая решение задачи минимизации затрат на трафик, положим, что искомая матрица расстояний фрагментов дуг соответствующих полных окружностей. Учитывая решение задачи минимизации затрат на трафик, положим, что искомая матрица расстояний  является поэлементным минимумом пары матриц расстояний является поэлементным минимумом пары матриц расстояний  и и 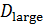 , т.е. , т.е. 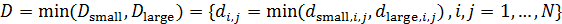 . .
Проведем вычислительный эксперимент по оценке среднего значения транспортных интегралов в формулах (32), (33). Для подсчета транспортных интегралов нам необходимы частные производные 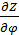 и и 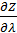 , которые вычислим с помощью конечных разностей в форме (17), (18) с разрешением рельефа , которые вычислим с помощью конечных разностей в форме (17), (18) с разрешением рельефа 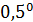 ; а также обыкновенные производные ; а также обыкновенные производные 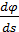 и и 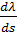 , которые найдем согласно (39), , которые найдем согласно (39),  . В остальном фрагмент полной окружности, соединяющий пару точек, делился на части, проходящие отдельно по суше и по морю. Для каждой части строилась конечно-разностная сетка с числом точек, равной величине . В остальном фрагмент полной окружности, соединяющий пару точек, делился на части, проходящие отдельно по суше и по морю. Для каждой части строилась конечно-разностная сетка с числом точек, равной величине  , где , где  — функция целой части числа, а пары — функция целой части числа, а пары  и и 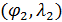 обозначают начало и конец (в градусах), рассматриваемой части. В дальнейшем в ряде случаев в целях экономии вычислительных ресурсов параметр 0,25 заменялся на 0,125. В итоге для каждой пары точек из общего числа обозначают начало и конец (в градусах), рассматриваемой части. В дальнейшем в ряде случаев в целях экономии вычислительных ресурсов параметр 0,25 заменялся на 0,125. В итоге для каждой пары точек из общего числа  вычислим транспортные интегралы и найдем средние значения из каждого набора. вычислим транспортные интегралы и найдем средние значения из каждого набора.
|
Таблица №7. Усредненные значения транспортных интегралов
|
|
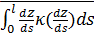
|
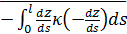
|
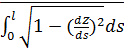
|
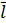
|
|
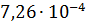
|
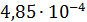
|
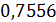
|
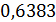
|
В таблице №7 приведен итог вычислительного эксперимента в формате, когда случайно согласно алгоритму раздела №6 выбиралось  точек и вычислялась матрица точек и вычислялась матрица  . Черта сверху во второй строке таблице №7 обозначает операцию усреднения. С учетом оценок из предыдущего раздела . Черта сверху во второй строке таблице №7 обозначает операцию усреднения. С учетом оценок из предыдущего раздела 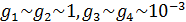 следует, что каждое слагаемое в (32), (33) с точки зрения средних значений вносит сравнимый вклад. В итоге остановимся на выборе значений параметров следует, что каждое слагаемое в (32), (33) с точки зрения средних значений вносит сравнимый вклад. В итоге остановимся на выборе значений параметров 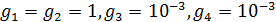 . .
Согласно определению в (32), (33) и таблице №7 интегралы берутся по маршруту, соединяющему пару точек на поверхности Земли. Поскольку все маршруты располагаются на одном из фрагментов полных окружностей, транспортные интегралы можно приближенно считать пропорциональными длине дуги. С этой точки зрения в среднем можно полагать, что матрица расстояний  совпадает с матрицей расстояний, найденной для малых фрагментов полных окружностей, т.е. считаем в дальнейшем, что совпадает с матрицей расстояний, найденной для малых фрагментов полных окружностей, т.е. считаем в дальнейшем, что 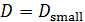 . .
9. Алгоритм минимизации транспортных издержек
Вернемся к задаче оптимизации транспортных издержек в форме  с учетом: 1) особенностей геометрии “суша – море” и 2) вычислительной трудоемкости подсчета функционала транспортных издержек с учетом: 1) особенностей геометрии “суша – море” и 2) вычислительной трудоемкости подсчета функционала транспортных издержек 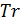 и, в особенности, его частных производных по и, в особенности, его частных производных по 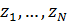 . Пусть на предыдущем шаге итерационной процедуры по формулам (35¢) подсчитаны объемы емкостей среды обитания, что позволяет определить функционал транспортных издержек . Пусть на предыдущем шаге итерационной процедуры по формулам (35¢) подсчитаны объемы емкостей среды обитания, что позволяет определить функционал транспортных издержек  в рамках текущей итерации. в рамках текущей итерации.
Для поиска минимума функции 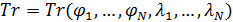 рассмотрим несколько модифицированную схему градиентного спуска. Запишем следующую систему обыкновенных дифференциальных уравнений: рассмотрим несколько модифицированную схему градиентного спуска. Запишем следующую систему обыкновенных дифференциальных уравнений:
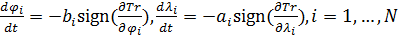 , (40) , (40)
где 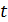 — некоторый вспомогательный аргумент, — некоторый вспомогательный аргумент,  , , 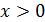 ; ; 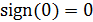 ; ; 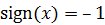 , ,  — так называемая “знаковая” функция, а наборы неотрицательных коэффициентов — так называемая “знаковая” функция, а наборы неотрицательных коэффициентов 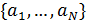 и и 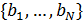 определим ниже. определим ниже.
Заменим обыкновенные производные в (40) на конечные разности, тогда
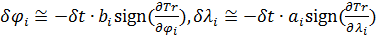 , (41) , (41)
где 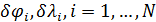 — конечные приращения функций, а — конечные приращения функций, а 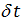 — конечное приращение аргумента. — конечное приращение аргумента.
С учетом (41) запишем алгоритм перехода от текущих значений функций 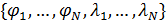 при значении аргумента при значении аргумента 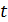 к новым значениям функций к новым значениям функций 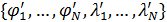 при значении аргумента при значении аргумента 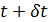 , а именно , а именно
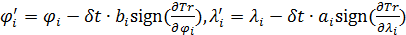 , , 
где 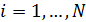 . Если после пересчета согласно алгоритму . Если после пересчета согласно алгоритму  одна или несколько точек выходят за пределы суши, уменьшаем соответствующие коэффициенты из наборов одна или несколько точек выходят за пределы суши, уменьшаем соответствующие коэффициенты из наборов 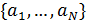 и и 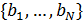 так, чтобы точки вернулись в пределы суши. В случае, если береговая линия не мешает движению точек, соответствующие значения коэффициентов полагаются равными единице. так, чтобы точки вернулись в пределы суши. В случае, если береговая линия не мешает движению точек, соответствующие значения коэффициентов полагаются равными единице.
Значение параметра 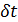 в (41), в (41), 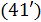 выбиралось из набора шагов выбиралось из набора шагов  вида: вида:
 , (42) , (42)
где 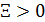 , , 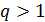 — некоторые константы, а — некоторые константы, а 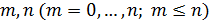 — натуральные значения. Конкретные значения параметров — натуральные значения. Конкретные значения параметров 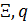 и и 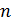 выбирались при проведении численных расчетов. выбирались при проведении численных расчетов.
С учетом (41¢), (42) подсчитаем новые положения точек 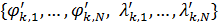 по формулам: по формулам:
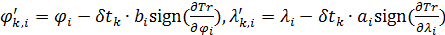 , (43) , (43)
с шагами  , а также значения функционала транспортных издержек: , а также значения функционала транспортных издержек:
 . (44) . (44)
Пусть в наборе (44) при просмотре слева направо находится номер  , при котором транспортные издержки становятся меньше тех, которые имели место на предыдущем шаге схемы градиентного спуска, т.е. , при котором транспортные издержки становятся меньше тех, которые имели место на предыдущем шаге схемы градиентного спуска, т.е.
 . (45) . (45)
В случае выполнения неравенства (45) при некотором 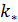 считается, что шаг градиентного спуска завершен и новые положения точек считаются равными: считается, что шаг градиентного спуска завершен и новые положения точек считаются равными:
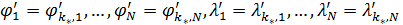 . (46) . (46)
Если неравенство (45) не выполняется при всех значениях  , то считается, что данный шаг процедуры градиентного спуска также завершен и новые положения точек выбираются равными: , то считается, что данный шаг процедуры градиентного спуска также завершен и новые положения точек выбираются равными:
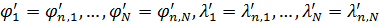 . . 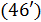
Для замыкания алгоритма минимизации (40) — 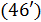 необходимо уточнить процедуру подсчета номера необходимо уточнить процедуру подсчета номера 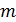 в наборе (42). Обозначим число в наборе (42). Обозначим число 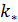 с предыдущего шага процедуры с предыдущего шага процедуры 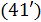 — — 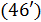 символом символом 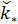 , тогда номер , тогда номер 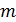 в наборе (42) подсчитаем по формуле: в наборе (42) подсчитаем по формуле: 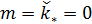 и и 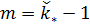 , ,  . .
Согласно алгоритму (40) —  необходимо иметь частные производные функции транспортных издержек необходимо иметь частные производные функции транспортных издержек 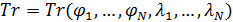 по координатам точек. Поскольку сделать это аналитически затруднительно, имеет смысл рассмотреть конечные разности. Введем некоторые приращения аргументов по координатам точек. Поскольку сделать это аналитически затруднительно, имеет смысл рассмотреть конечные разности. Введем некоторые приращения аргументов 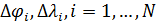 и запишем следующие выражения: и запишем следующие выражения:
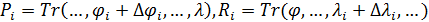 , (47) , (47)
где 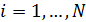 . При этом, как и выше, будем считать, что N точек с координатами . При этом, как и выше, будем считать, что N точек с координатами 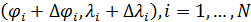 находятся в пределах суши. Если это не так варьируем приращения находятся в пределах суши. Если это не так варьируем приращения 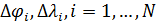 . С учетом (47) положим, что . С учетом (47) положим, что
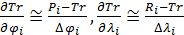 . (48) . (48)
Выполняем процедуру градиентного спуска (40) — (48) до тех пор, пока интегральные издержки на трафик понижаются. Если дальнейшее понижение трафика не удается, считаем согласно формуле  , что найдены новые положения N точек , что найдены новые положения N точек 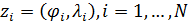 . Пересчитываем по новым значениям N точек объемы емкостей среды обитания . Пересчитываем по новым значениям N точек объемы емкостей среды обитания 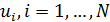 соответствующих многоугольников Вороного. Переходим к следующему шагу, т.е. к оптимизационной процедуре (40) — (48). соответствующих многоугольников Вороного. Переходим к следующему шагу, т.е. к оптимизационной процедуре (40) — (48).
Невозможность дальнейшего понижения трафика означает, что шаг градиентного спуска  становится минимальным и равным становится минимальным и равным 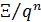 , а доля вариации затрат на трафик за один шаг градиентного спуска периодически меняет знак так, что интегральные затраты на трафик колеблются возле некоторого постоянного значения. , а доля вариации затрат на трафик за один шаг градиентного спуска периодически меняет знак так, что интегральные затраты на трафик колеблются возле некоторого постоянного значения.
В процедуре градиентного спуска (40) — (48) с целью понижения вариабельности при конечно-разностном подсчете производных транспортных издержек (47), (48), было проведено сглаживание рельефа с помощью процедуры скользящих средних. Усреднение проводилось по ближайшим соседям в области квадратной формы в координатах “широта – долгота” с числом точек  , при этом исходная матрица рельефа имела разрешение , при этом исходная матрица рельефа имела разрешение 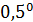 и была представлена в форме матрицы размером и была представлена в форме матрицы размером 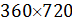 . .
Для исходной оценки параметра 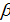 , входящего в формулы , входящего в формулы 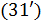 , (34), , (34),  , будем исходить из приближенной оценки доли транспортных затрат в мировом ВВП в диапазоне от 4% до 15% в зависимости от развитости транспортной инфраструктуры. В расчетах будем полагать эту долю, равной приблизительно 10%. , будем исходить из приближенной оценки доли транспортных затрат в мировом ВВП в диапазоне от 4% до 15% в зависимости от развитости транспортной инфраструктуры. В расчетах будем полагать эту долю, равной приблизительно 10%.
Параметр 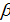 оценим, исходя из формулы оценим, исходя из формулы 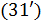 , полагая, что затраты на трафик составляют некоторую долю , полагая, что затраты на трафик составляют некоторую долю 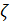 от всей емкости среды обитания, т.е. от всей емкости среды обитания, т.е.
 . (49) . (49)
Считая заданными: константу 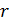 , набор , набор 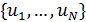 , матрицу , матрицу 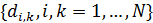 и долю и долю 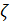 решим уравнение (50) и найдем коэффициент решим уравнение (50) и найдем коэффициент 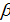 , который должен обеспечить на финальной стадии процесса минимизации , который должен обеспечить на финальной стадии процесса минимизации  , , 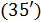 долю трафика от всей емкости среды обитания в окрестности 10%. долю трафика от всей емкости среды обитания в окрестности 10%.
|
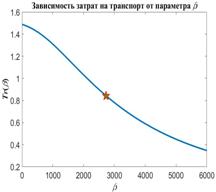
|
|
|
Рис.19,а. Зависимость затрат на транспорт от параметра 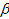
|
Рис.19,б. Многоугольники Вороного для начального распределения c 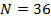 точек точек
|
На рис.19,а согласно (49) построен типичный пример графика функции 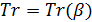 при при 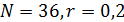 . Пентаграммой на графике отмечено значение параметра . Пентаграммой на графике отмечено значение параметра 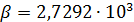 , которое получено путем решения уравнения (49) при , которое получено путем решения уравнения (49) при 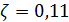 . Матрица расстояний . Матрица расстояний 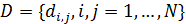 была подсчитана по случайному набору точек, полученному согласно алгоритму раздела №6. На рис.19,б приведены позиции случайного начального распределение точек (обозначены центрами маркеров в виде окружностей o) на поверхности Земли, а также соответствующие многоугольники Вороного. была подсчитана по случайному набору точек, полученному согласно алгоритму раздела №6. На рис.19,б приведены позиции случайного начального распределение точек (обозначены центрами маркеров в виде окружностей o) на поверхности Земли, а также соответствующие многоугольники Вороного.
На рис.20,а,б приведена динамика зависимости транспортных затрат от номера шага градиентного спуска согласно процедуре (40) — (48) с параметрами:  , , 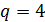 , , 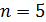 для двух наборов точек числом 36 и 72 соответственно. для двух наборов точек числом 36 и 72 соответственно.
|
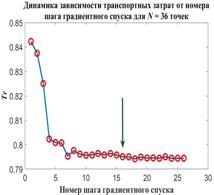
|
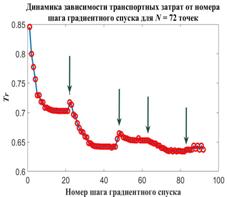
|
|
Рис.20,а. Динамика зависимости транспортных затрат от номера шага градиентного спуска для 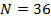 точек точек
|
Рис.20,б. Динамика зависимости транспортных затрат от номера шага градиентного спуска 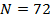 точек точек
|
Для 36 точек в целом было осуществлено 26 шагов процедуры (40) — (48), затраты на трафик при этом уменьшились на 5,7% по сравнению с исходным значением. Окружностями на рис.20,а,б обозначены значения транспортных затрат после каждого шага процедуры градиентного спуска. Итоговая доля затрат на трафик для 36 точек по отношению ко всей емкости среды обитания составила 10,4%. В течение всего расчета один раз пересчитывался набор емкостей среды обитания  . На рис.20,а,б места пересчета обозначены стрелками. На завершающей стадии расчетов на рис.20,а,б виден выход значений трафика на некоторое плато. . На рис.20,а,б места пересчета обозначены стрелками. На завершающей стадии расчетов на рис.20,а,б виден выход значений трафика на некоторое плато.
На рис.21 приведен итог расчета положений 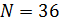 точек после применения процедуры оптимизации затрат на транспорт (40) — (48) и одного пересчета набора емкостей среды обитания, ассоциированных с каждой из точек. Первоначально точки выбирались случайно согласно алгоритму (21) — (24), они помечены центрами маркеров в виде синих окружностей (o) на рис.19,б и на рис.21. После применения процедуры оптимизации точек после применения процедуры оптимизации затрат на транспорт (40) — (48) и одного пересчета набора емкостей среды обитания, ассоциированных с каждой из точек. Первоначально точки выбирались случайно согласно алгоритму (21) — (24), они помечены центрами маркеров в виде синих окружностей (o) на рис.19,б и на рис.21. После применения процедуры оптимизации  , , 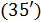 , (40) — (48) положение точек помечено маркерами в виде пентаграмм. Максимумы смещений составили , (40) — (48) положение точек помечено маркерами в виде пентаграмм. Максимумы смещений составили  и и 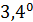 по широте и долготе соответственно. по широте и долготе соответственно.
На карте рис.21 маркерами в виде крестиков  помечены крупнейшие города (координаты городов взяты из базы данных, содержащейся в Matlab Mapping Toolbox) на Земле в количестве 318. Отмечены названия 7-и городов, координаты которых были наиболее близки к итоговым позициям помечены крупнейшие города (координаты городов взяты из базы данных, содержащейся в Matlab Mapping Toolbox) на Земле в количестве 318. Отмечены названия 7-и городов, координаты которых были наиболее близки к итоговым позициям 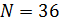 точек. С учетом (38), точек. С учетом (38), 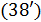 в качестве критерия отбора городов выбиралось условие того, что угловое расстояние в качестве критерия отбора городов выбиралось условие того, что угловое расстояние 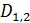 между парой точек между парой точек 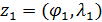 , , 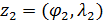 было меньше одного градуса, т.е. было меньше одного градуса, т.е. 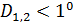 , где , где 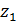 — координаты одного из городов из набора, а — координаты одного из городов из набора, а 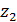 — одна из позиций, обозначенных маркерами в виде пентаграмм. — одна из позиций, обозначенных маркерами в виде пентаграмм.
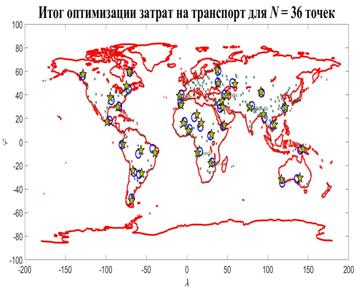
Рис.21. Итог оптимизации затрат на транспорт для  точек, вначале случайно позиционированных на поверхности Земли точек, вначале случайно позиционированных на поверхности Земли
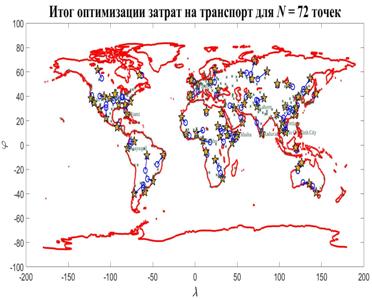
Рис.22. Итог оптимизации затрат на транспорт для 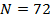 точек, вначале случайно позиционированных на поверхности Земли точек, вначале случайно позиционированных на поверхности Земли
Дальнейшая апробация алгоритма оптимизации транспортных затрат 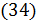 , ,  (40) — (48) была проведена после удвоения числа точек, т.е. при (40) — (48) была проведена после удвоения числа точек, т.е. при  . На рис.20,б приведена динамика зависимости транспортных затрат от номера шага градиентного спуска. Всего было проведено 88 шагов градиентного спуска (40) — (48) и четыре пересчета набора емкостей среды обитания по формуле . На рис.20,б приведена динамика зависимости транспортных затрат от номера шага градиентного спуска. Всего было проведено 88 шагов градиентного спуска (40) — (48) и четыре пересчета набора емкостей среды обитания по формуле 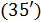 . Иные параметры процедуры составили следующие значения: . Иные параметры процедуры составили следующие значения: 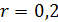 ; ; 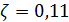 ; ; 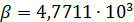 ; ; 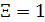 ; ; 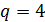 ; ; 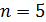 . После проведения процедуры оптимизации затраты на трафик уменьшились на 24,6%, доля трафика по отношению ко всей емкости среды обитания составила 8,3%. . После проведения процедуры оптимизации затраты на трафик уменьшились на 24,6%, доля трафика по отношению ко всей емкости среды обитания составила 8,3%.
На рис.22 приведен итог оптимального позиционирования  точек. Начальные позиции точек обозначены маркерами в виде голубых окружностей (o), центры положения которых выбраны случайно согласно алгоритму (21) — (24). Финальные, оптимальные положения точек обозначены маркерами в виде пентаграмм. Максимальная вариабельность позиций точек по широте и долготе не превысила значений точек. Начальные позиции точек обозначены маркерами в виде голубых окружностей (o), центры положения которых выбраны случайно согласно алгоритму (21) — (24). Финальные, оптимальные положения точек обозначены маркерами в виде пентаграмм. Максимальная вариабельность позиций точек по широте и долготе не превысила значений 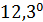 и и 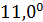 соответственно. Отмечены названия 10-и городов, координаты которых были в пределах одного углового градуса к итоговым позициям соответственно. Отмечены названия 10-и городов, координаты которых были в пределах одного углового градуса к итоговым позициям  точек. На карте рис.22 стрелками соединены начальные и конечные после процедуры оптимизации позиции точек, угловое расстояние между которыми превысило значение точек. На карте рис.22 стрелками соединены начальные и конечные после процедуры оптимизации позиции точек, угловое расстояние между которыми превысило значение 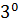 . .
Сравнивая рис.21 и рис.22 можно отметить следующее. Оптимальные положения точек (маркеры в виде пентаграмм) стремятся заполнить всю емкость среды обитания, т.е. стремятся распределиться по возможности равномерно на поверхности Земли с учетом неравномерной плотности емкости среды обитания. Таким образом, расчеты оптимального позиционирования точек, приведенные на рис.21,22, подтверждают реализацию минимаксной транспортной доктрины.
10. Геополитическая классификация точек и территорий
Перейдем к задаче идентификации позиционирования набора точек в пределах суши в терминах морского или континентального типов. Для этого определим процентное соотношение “моря – континент” в глобальном трафике, SeaContinent. Учитывая формулы для транспортных интегралов (32), (33), запишем следующее соотношение:
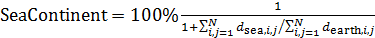 , (50) , (50)
где  и и  — суммарные части расстояний, проходящих по морю и суше для пары точек с номерами — суммарные части расстояний, проходящих по морю и суше для пары точек с номерами  и и  . .
Процентное соотношение (50) нормировано следующим образом. Пусть суммы расстояний, проходящих по морю равны нулю, т.е. 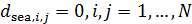 , тогда процентное соотношение равно 100%, т.е. , тогда процентное соотношение равно 100%, т.е. 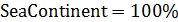 . В этом случае можно говорить о чисто морском типе трафика. С точки зрения затрат на транспорт условие равенства нулю части обобщенного расстояния означает, что затраты на транспорт на этом участке отсутствуют. . В этом случае можно говорить о чисто морском типе трафика. С точки зрения затрат на транспорт условие равенства нулю части обобщенного расстояния означает, что затраты на транспорт на этом участке отсутствуют.
В случае, когда суммы расстояний, проходящих по суше равны нулю, т.е. 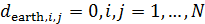 , процентное соотношение равно нулю, т.е. , процентное соотношение равно нулю, т.е. 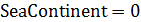 . В данном случае имеем дело с чисто континентальным типом трафика. Аналогично процентному соотношению (50), нормированному на морской тип трафика, можно ввести процентное соотношение, . В данном случае имеем дело с чисто континентальным типом трафика. Аналогично процентному соотношению (50), нормированному на морской тип трафика, можно ввести процентное соотношение,
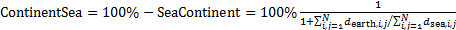 , , 
нормированное на континентальный тип трафика.
Процентные соотношения (50),  можно изменять двумя способами. Во-первых, варьируя параметры можно изменять двумя способами. Во-первых, варьируя параметры 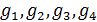 , которые характеризуют транспортные интегралы (32), (33). Во-вторых, путем вариации позиций точек в связи с процедурой оптимизации затрат на трафик. Оптимизационная процедура трафика была рассмотрена в предыдущем разделе. , которые характеризуют транспортные интегралы (32), (33). Во-вторых, путем вариации позиций точек в связи с процедурой оптимизации затрат на трафик. Оптимизационная процедура трафика была рассмотрена в предыдущем разделе.
Перепишем процентное соотношение (50) с явным выделением параметров 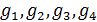 . Для этого введем обозначения для четырех транспортных интегралов, . Для этого введем обозначения для четырех транспортных интегралов, 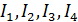 , входящих в (32), (33), т.е. , входящих в (32), (33), т.е.
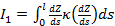 , , 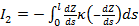 , , 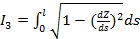 , , 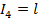 . (51) . (51)
Представим процентное соотношение (50) с учетом транспортных интегралов (51), тогда
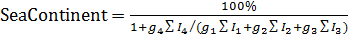 , (52) , (52)
где 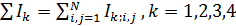 , а , а 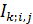 — —  -й транспортный интеграл между парой точек -й транспортный интеграл между парой точек 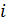 и и 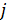 . .
В таблице №8 приведены результаты подсчета процентного соотношения (50) для числа точек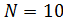 и и 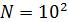 соответственно. В десяти вычислительных экспериментах позиции точек были сгенерированы случайно согласно процедуре раздела №6. соответственно. В десяти вычислительных экспериментах позиции точек были сгенерированы случайно согласно процедуре раздела №6.
|
Таблица №8. Результаты подсчета процентного соотношения “море – континент” для случайно позиционированных точек, когда 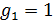 , , 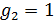 , , 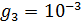 , , 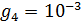
|
|
|
№1
|
№2
|
№3
|
№4
|
№5
|
|

|
89,9%
|
85,0%
|
63,0%
|
69,9%
|
73,9%
|
|
|
69,8%
|
68,7%
|
68,2%
|
69,0%
|
68,0%
|
Из анализа значений процентного соотношения по таблице №8 вытекают следующие выводы. Во-первых, при выбранных значениях параметров 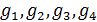 имеем дело преимущественно с морским типом трафика ( имеем дело преимущественно с морским типом трафика ( ). Это не удивительно, т.к. поверхность Земли, как известно, подразделяется на сушу и море в отношении 29,2% и 70,8% соответственно. Во-вторых, уже при числе точек, превышающих ). Это не удивительно, т.к. поверхность Земли, как известно, подразделяется на сушу и море в отношении 29,2% и 70,8% соответственно. Во-вторых, уже при числе точек, превышающих 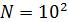 , вариабельность процентного соотношения резко снижается. Это означает, что, если не принимать в расчет специально подобранную геометрию позиционирования точек, то процентное соотношение можно значительно изменить только за счет вариации параметров , вариабельность процентного соотношения резко снижается. Это означает, что, если не принимать в расчет специально подобранную геометрию позиционирования точек, то процентное соотношение можно значительно изменить только за счет вариации параметров 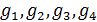 . .
В дополнение к таблице №8 рассмотрим случай, когда 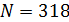 . В качестве набора точек рассмотрим, упомянутую в предыдущем разделе базу данных по 318-и крупнейшим городам Земли. После подсчета для них процентного соотношения (50) с параметрами . В качестве набора точек рассмотрим, упомянутую в предыдущем разделе базу данных по 318-и крупнейшим городам Земли. После подсчета для них процентного соотношения (50) с параметрами 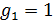 , , 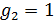 , , 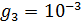 , , 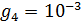 оказалось, что оно равно 73,17%. Полученное значение несколько выше современной оценки доли морского транспорта в глобальном трафике, равной 2/3. Изменим параметр оказалось, что оно равно 73,17%. Полученное значение несколько выше современной оценки доли морского транспорта в глобальном трафике, равной 2/3. Изменим параметр 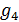 так, чтобы обеспечить процентное соотношение равным 2/3 или 66,67%. Для этого выразим из уравнения (52) параметр так, чтобы обеспечить процентное соотношение равным 2/3 или 66,67%. Для этого выразим из уравнения (52) параметр 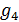 через три другие параметра через три другие параметра  , тогда , тогда
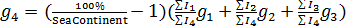 . (53) . (53)
После подстановки в (53) для выбранных значений 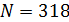 точек-городов точек-городов 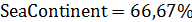 , а также найденных с помощью вычислительного эксперимента величин: , а также найденных с помощью вычислительного эксперимента величин: 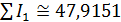 ; ; 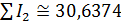 ; ; 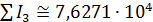 ; ; 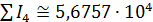 , получим , получим
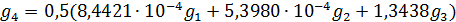 . . 
Подставляя в  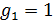 , , 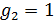 , , 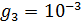 , найдем модифицированное значение параметра , найдем модифицированное значение параметра  , которое обеспечивает процентное соотношение, равным 66,67% (до процедуры минимизации транспортных затрат). , которое обеспечивает процентное соотношение, равным 66,67% (до процедуры минимизации транспортных затрат).
По аналогии с (50) сконструируем процентное соотношение для каждой точки из некоторого набора. Учитывая, что матрицы  и и  , , 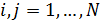 вообще говоря не являются симметричными, составим следующее процентное соотношение: вообще говоря не являются симметричными, составим следующее процентное соотношение:
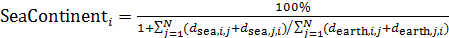 , (54) , (54)
где  . Процентное соотношение (54) позволяет оценить соотношение “море – континент” применительно к каждой точке из заданного набора. . Процентное соотношение (54) позволяет оценить соотношение “море – континент” применительно к каждой точке из заданного набора.
С учетом определения в (54) классифицируем 318 точек – городов в терминах предпочтений “море – континент”. После оценки в (53),  глобального процентного соотношения, равного 66,67%, стало понятно, что это значение выступает в качестве разделителя предпочтений в связке “море – континент”. Другими словами, если для некоторой глобального процентного соотношения, равного 66,67%, стало понятно, что это значение выступает в качестве разделителя предпочтений в связке “море – континент”. Другими словами, если для некоторой 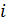 -ой точки -ой точки 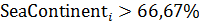 , то данное обстоятельство истолкуем в том смысле, что , то данное обстоятельство истолкуем в том смысле, что 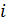 -я точка ориентирована на море. И, наоборот, если некоторая -я точка ориентирована на море. И, наоборот, если некоторая  -я точка такова, что -я точка такова, что  , то это будет означать, что , то это будет означать, что  -я точка ориентирована на континент. Слово “ориентация” истолкуем в смысле геополитического противостояния, т.е. “море” стремится к власти над “континентом” и, наоборот, “континент” стремится овладеть “морем”. -я точка ориентирована на континент. Слово “ориентация” истолкуем в смысле геополитического противостояния, т.е. “море” стремится к власти над “континентом” и, наоборот, “континент” стремится овладеть “морем”.
Отметим следующее важное обстоятельство в вопросе противостояния моря и континента. Если некоторая  -я точка ориентирована на море, то это означает, что она укоренена в континенте или, иначе, позиционирована континентально. И, наоборот, если -я точка ориентирована на море, то это означает, что она укоренена в континенте или, иначе, позиционирована континентально. И, наоборот, если  -я точка ориентирована на континент, то это означает, что она укоренена в море или, иначе, имеет морское позиционирование. Таким образом, каждая точка (соответствующая территория) имеет два атрибута: 1) ориентацию и 2) позиционирование. С точки зрения геополитики оба атрибута применительно к каждой точке имеют противоположные наименования в терминах “море – континент”. Это означает, что если имеет место морская ориентация, то позиционирование — континентальное и, наоборот. Атрибут “ориентация” характеризуется процентным соотношением -я точка ориентирована на континент, то это означает, что она укоренена в море или, иначе, имеет морское позиционирование. Таким образом, каждая точка (соответствующая территория) имеет два атрибута: 1) ориентацию и 2) позиционирование. С точки зрения геополитики оба атрибута применительно к каждой точке имеют противоположные наименования в терминах “море – континент”. Это означает, что если имеет место морская ориентация, то позиционирование — континентальное и, наоборот. Атрибут “ориентация” характеризуется процентным соотношением  ; атрибут “позиционирование” — процентным соотношением ; атрибут “позиционирование” — процентным соотношением  . Эти вербальные формулы следует понимать в метафорическом смысле, т.к. все точки, имеющие как морской, так и континентальный тип ориентации, базируются на суше. . Эти вербальные формулы следует понимать в метафорическом смысле, т.к. все точки, имеющие как морской, так и континентальный тип ориентации, базируются на суше.
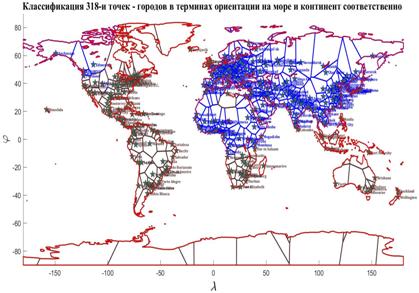
Рис.23. Классификация 318-точек – городов в терминах ориентации на море (синий цвет) и континент (коричневый цвет) соответственно
На рис.23 приведен итог вычислительного эксперимента по подсчету процентных соотношений (54) для каждой из 318-и точек – городов. При вычислении транспортных интегралов выбирались следующие значения параметров: 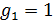 , , 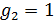 , , 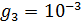 , ,  . На рис.23 приведена карта-классификация 318-и точек – городов в терминах их ориентации, либо на море, либо на континент. Точки – города помечены маркерами в виде пентаграмм, окруженных подходящими многоугольниками Вороного. Города и регионы, ориентированные на море помечены синим цветом; города и регионы, помеченные коричневым цветом, ориентированы на континент. . На рис.23 приведена карта-классификация 318-и точек – городов в терминах их ориентации, либо на море, либо на континент. Точки – города помечены маркерами в виде пентаграмм, окруженных подходящими многоугольниками Вороного. Города и регионы, ориентированные на море помечены синим цветом; города и регионы, помеченные коричневым цветом, ориентированы на континент.
Согласно карте рис.23 существует огромное скопление регионов, помеченный синим цветом, которые ориентированы на море. Данное скопление назовем “Континент”, он состоит из Европы, Азии, Северной и Экваториальной Африк, а также из небольшого фрагмента в Северной Америке. Континент окружен множеством разбросанных территорий, которые состоят из почти всей Северной Америки, Южной Америки, Южной Африки, Австралии, Новой Зеландии и Океании. К этой же группе необходимо также отнести и Антарктиду. Все эти регионы ориентированы на континент, т.е. они имеют морское позиционирование. В этой связи назовем всю совокупность территорий, имеющих морское позиционирование “Морем”.
На рис.24,а,б приведены отдельные фрагменты карты рис.23, на которых выделены два особых случая смешения территорий с противоположной ориентацией. На рис.24,а приведена Северная Америка, в которой все территории ориентированы на Континент кроме шести. К этим шести относятся территории, ассоциированные с такими городами, как Анкоридж (69,1%), Ванкувер (67,8%), Сиэтл (67,5%), Портленд (67,1%), Эдмонтон (69,3%) и Денвер (67,9%). На рис.24,б приведена Европа и Северная Африка, в которой все территории ориентированы на море кроме четырех. К этим четырем относятся территории, ассоциированные с такими городами, как Дублин (64,8%), Глазго (64,8%), Эдинбург (64,6%) и Триполи (66,66%). Значение процентного соотношения 66,66% для Триполи незначительно меньше порогового значения 66,67%, т.е. территория, ассоциированная с Триполи, является пограничной между двумя противоположными ориентациями.
|
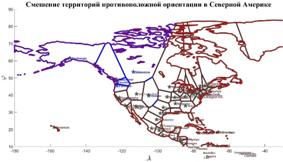
|
|
|
Рис.24,а. Смешение территорий противоположной ориентации в Северной Америке
|
Рис.24,б. Смешение территорий противоположной ориентации в Англии и Северной Африке
|
Отметим, что все, перечисленные выше, ориентации (на море, на континент) территорий следует трактовать с точки зрения геополитики. Вердикт о той или иной ориентации города (территории) получен путем вычисления процентного соотношения (54), которое сравнивалось с глобальным процентным соотношением, равным 66,67%.
Сравним суммарную емкость среды обитания территорий, ориентированных на море, 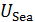 , с суммарной емкостью среды обитания территорий, ориентированных на континент, , с суммарной емкостью среды обитания территорий, ориентированных на континент, 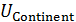 . Указанные величины подсчитаем по формулам: . Указанные величины подсчитаем по формулам:
 , , 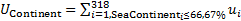 , (55) , (55)
где 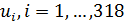 — емкости среды обитания каждого из 318-и многоугольников Вороного, внешний вид которых приведен на рис.23,24. В суммах (55) учитывались лишь те слагаемые, процентные соотношения которых удовлетворяли соответствующим неравенствам. — емкости среды обитания каждого из 318-и многоугольников Вороного, внешний вид которых приведен на рис.23,24. В суммах (55) учитывались лишь те слагаемые, процентные соотношения которых удовлетворяли соответствующим неравенствам.
После подсчета величин (55) оказалось, что 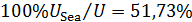 , , 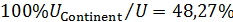 , где , где  — глобальная емкость среды обитания. Таким образом, потенциал геополитического противостояния между территориями, ориентированными на море и континент находятся в пропорции 51,73% к 48,27%, т.е. приблизительно поровну. — глобальная емкость среды обитания. Таким образом, потенциал геополитического противостояния между территориями, ориентированными на море и континент находятся в пропорции 51,73% к 48,27%, т.е. приблизительно поровну.
Построим аналоги скоплений территорий под называнием “Хартленд” и “Римленд”. Эти понятия характерны для классической геополитики, они введены в первой половине ХХ века Х.Дж. Маккиндером и Н. Спикменом соответственно. Определим также место, где проходит пресловутая географическая “ось” истории.
Согласно рис.23 континентально позиционированные территории (соответствующие многоугольники Вороного) определяются из условия того, что индивидуальное процентное соотношение больше 66,67%. Пусть таких территорий 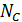 . Найдем среди этих территорий среднее значение процентного соотношения, . Найдем среди этих территорий среднее значение процентного соотношения, 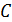 по следующей формуле: по следующей формуле:
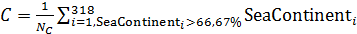 . (56) . (56)
Наличие среднего процентного соотношения, вычисленного согласно (56), позволяет разделить территории на две категории, у которых индивидуальные процентные соотношения находятся в двух диапазонах:  и и 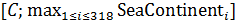 . Территории, попадающие в первый диапазон, отнесем к Римленду, а во второй диапазон — к Хартленду. . Территории, попадающие в первый диапазон, отнесем к Римленду, а во второй диапазон — к Хартленду.
В качестве кандидатов на географическое место “оси” истории с помощью средневзвешенного среднего определим две точки. В качестве весов будут выступать соответствующие значения емкостей среды обитания каждой из территорий.
Первая точка выступает в качестве центра “тяжести” для всех территорий, ориентированных на море или континентально позиционированных. Позицию 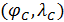 этой точки найдем согласно формулам: этой точки найдем согласно формулам:
 , ,  . (57) . (57)
Вторая точка выступает в качестве центра тяжести для всех территорий, относимых к Хартленду. Позицию 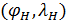 этой точки найдем согласно формулам: этой точки найдем согласно формулам:
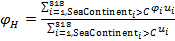 , ,  . (58) . (58)
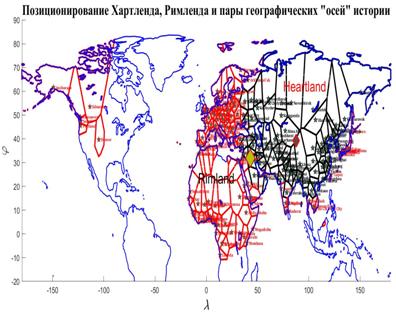
Рис.25. Позиционирование Хартленда, Римленда и пары географических “осей” истории
В рамках изложенных выше модельных соображений, построим карту с Римлендом, Хартлендом и парой точек (57), (58), претендентов на географическую “ось” истории. На рис.25 приведен итог. Черным цветом выделены территории, относимые к Харленду, красным цветом выделены территории, относимые к Римленду.
Оказалось, что разделителем территорий на Римленд и Хартленд выступает значение процентного соотношения, равного 73,7%, т.к. 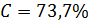 . При этом в Харленд попало 83 территории, а в Римленд — 119, итого . При этом в Харленд попало 83 территории, а в Римленд — 119, итого  . В терминах емкости среды обитания доли Хартленда и Римленда в Континенте составили 47,52% и 52,48% соответственно. . В терминах емкости среды обитания доли Хартленда и Римленда в Континенте составили 47,52% и 52,48% соответственно.
Наконец были вычислены и нанесены на карту (два маркера в виде ромбов) две точки обозначающие географические “оси” истории. Более крупный ромб обозначает точку с координатами  , , 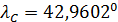 , которые соответствуют гор. Кербела в Ираке. Менее крупный ромб обозначает точку с координатами , которые соответствуют гор. Кербела в Ираке. Менее крупный ромб обозначает точку с координатами  , , 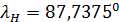 , которые соответствуют безымянной позиции в Синьцзян-Уйгурском автономном районе Китая. , которые соответствуют безымянной позиции в Синьцзян-Уйгурском автономном районе Китая.
В силу важности с точки зрения геополитики понятий “Хартленд” и “Римленд”, определим внутри Хартленд и Римленд подразделение на две группы регионов относительно соответствующих средних значений процентных соотношений. Другими словами, разделим Харленд на Хартленд 1 и Хартленд 2 и, аналогично, Римленд на Римленд 1 и Римленд 2.
На рис.26 приведена карта, на которой построено искомое подразделение на два Хартленда, причем Хартленд 1 имеет более высокое значение процентного соотношения  , чем Хартленд 2. На карте границы территорий, относимых к категории Хартленд 1 окрашены в черный цвет, границы территорий, относимых к категории Хартленд 2 окрашены в темно-красный цвет. , чем Хартленд 2. На карте границы территорий, относимых к категории Хартленд 1 окрашены в черный цвет, границы территорий, относимых к категории Хартленд 2 окрашены в темно-красный цвет.
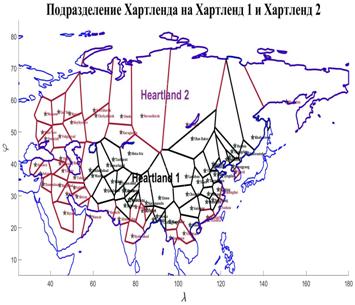
Рис.26. Подразделение Хартленда на Хартленд 1 и Хартленд 2
Изучение карты рис.26 приводит к неожиданным для классической геополитики выводам. Внутри Континента имеется компактное ядро, названное Хартленд 1, которое окружено поясом, названным Хартленд 2. К Хартленду 1 можно отнести Центральную Азию, Тибет, большую часть Китая, часть РФ.
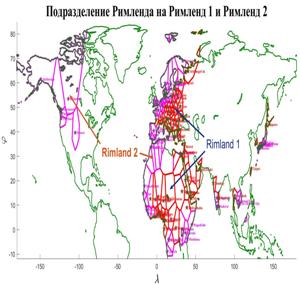
Рис.27. Подразделение Римленда на Римленд 1 и Римленд 2
На рис.27 приведена карта, на которой построено искомое подразделение на два Римленда, причем Римленд 1 имеет более высокое значение процентного соотношения  , чем Римленд 2. На карте границы территорий, относимых к категории Римленд 1 окрашены в красный цвет, границы территорий, относимых к категории Римленд 2 окрашены в пурпурный (magenta) цвет. , чем Римленд 2. На карте границы территорий, относимых к категории Римленд 1 окрашены в красный цвет, границы территорий, относимых к категории Римленд 2 окрашены в пурпурный (magenta) цвет.
Изучение карты рис.27 говорит о сильной неодносвязности, как Римленд 1, так и Римленд 2. В Римленд 1 можно обнаружить два крупных, компактных скопления, это Центральная Европа и Центральная Африка.
Осталось более подробно изучить внутреннюю структуру территорий, ориентированных на континент, т.е. позиционированных, как морские. Для этих территорий индивидуальное процентное соотношение меньше или равно 66,67%. Поделим эти территории на два класса относительно соответствующего среднего значения процентных соотношений. Назовем эти два класса территорий “Римленд 3” и “Римленд 4”. При этом процентные соотношения территорий Римленда 3 больше процентных соотношений Римленда 4.
На рис.28 приведена карта, на которой построено искомое подразделение на два класса: Римленд 3 и Римленд 4. На карте границы территорий, относимых к категории Римленд 3 окрашены в красный цвет, границы территорий, относимых к категории Римленд 4 окрашены в пурпурный (magenta) цвет.
Обращает на себя внимание на карте рис.28 отнесение США, большей части Канады, средней части Южной Америки, а также Южной Африки к Римленду 3. Наконец, центральная Америка, юг Южной Америки, Австралия и большая часть Антарктики входят в Римленд 4.
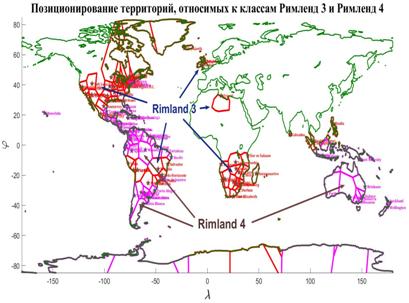
Рис.28. Позиционирование территорий, относимых к классам Римленд 3 и Римленд 4
Найдем пару территорий из нашего перечня, которые отвечают максимальному и минимальному значениям процентного соотношения. На рис.29 приведен результат. На рис.29,а приведен город Ланьчжоу (Lanzhou) и соответствующая территория, которые имеют максимальное значение процентного соотношения, равного 82,84%. На рис.29,б приведен город Окленд (Auckland) и соответствующая территория, которые имеют минимальное процентное соотношение, равное 39,15%. Данные города и территории из выбранного перечня максимально удалены друг от друга в геополитическом смысле слова, при этом гор. Ланьчжоу находится в Хартленд 1, а гор. Окленд — в Римленд 4.
|

|

|
|
Рис.29,а. Позиционирование точки и территории, имеющей максимальное значение процентного соотношения
|
Рис.29,б. Позиционирование точки и территории, имеющей минимальное значение процентного соотношения
|
Соберем вместе нашу классификацию точек и территорий в терминах геополитики. Итог представлен в виде таблицы №9.
В таблице №9 собрана номенклатура 6 классов точек и территорий, названных в терминах геополитики. Приведены интервалы значений процентного соотношения точек (территорий), который характеризуют тот или иной класс. В последней строке таблицы №9 приведены емкости среды обитания каждого из классов, а также сумма всех частных емкостей, равная глобальной емкости среды обитания  . .
|
Таблица №9. Итоговая геополитическая классификация точек и территорий
|
|
Номенклатура классов
|
Море
|
Континент
|
|
Римленд
|
Хартленд
|
|
Римленд 4
|
Римленд 3
|
Римленд 2
|
Римленд 1
|
Хартленд 2
|
Хартленд 1
|
|
SeaContinent, %
|

|
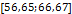
|
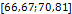
|
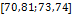
|
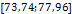
|
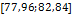
|
|
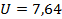
|
1,5865
|
2,1010
|
0,9404
|
1,1339
|
0,9538
|
0,9244
|
С учетом таблицы №9 построим карту, на которой проведем геополитические линии, отделяющие Хартленд 1, Хартленд 2, Римленд 1, Римленд 2, Римленд 3, Римленд 4. Другими словами, построим карту представляющую геополитическое строение поверхности Земли согласно данной модели. Итог приведен на рис.30.
Совместим карту геополитического строения Земли, приведенную на рис.30, с текущей политической картой мира. Это позволит построить перечень государств, через территорию которых проходят те или иные геополитических линии. Эти линии можно будет трактовать в качестве “разломов” с учетом всей текущей и, быть может, прошлой истории отдельного государства данного перечня. Поскольку на одной карте совместить все эти линии крайне затруднительно рассмотрим некоторые фрагменты глобальной карты.
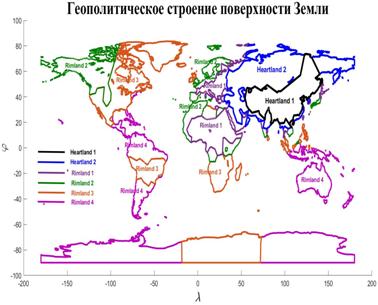
Рис.30. Геополитическое строение поверхности земли
Построим отдельно Хартленд плюс государственные границы ассоциированных стран. На рис.31 приведен итог. После изучения данной карты можно заключить следующее. Россия практически полностью входит в Хартленд, точнее в Хартленд 2, есть лишь небольшие пересечения с Римлендом 1. Китай практически полностью входит в Хартленд 1. Через Украину с севера на юг проходит линия, разделяющая Римленд 1 и Хартленд 2. С учетом текущих и прошлых событий на Украине можно сделать заключение, что линия, разделяющая Римленд 1 и Хартленд 2 является линией геополитического разлома. Любопытно что эта же линия пересекает и Турцию, причем в Римленде 1 оказывается где-то треть территории Турции, а в Хартленде 2 — две трети. Эта же линия частью проходит по территории Сирии. Оказывается, что Оман относится к Хартленду 2. Та же линия разлома проходит по территории Тайланда, рассекая ее практически пополам. Оказывается, что Тайвань относится к Римленду 1. С Корейским полуостровом особенно любопытно, по нему проходят две линии: первая линия отделяет Хартленд 1 от Хартленда 2, вторая линия отделяет Хартленд 2 от Римленд 1. Отметим, что первая линия довольно близка линии разделяющей две Кореи. Наконец, что довольно любопытно, Япония практически пополам делиться линией, разделяющей Римленд 1 и Римленд 2. Данная линия не рассматривается в качестве линии геополитического разлома.
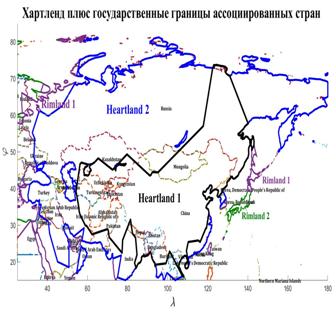
Рис.31. Хартленд плюс государственные границы ассоциированных стран
Совместим политическую карту Европы и геополитические линии, определенные на рис.30. На рис.32 приведена искомая карта.
Визуальный осмотр карты рис.32 показывает, что внутри Европы есть ядро, именуемое Римленд 1, окруженное территориями, именуемыми Римленд 2. Линия, отделяющая Римленд 1 и Римленд 2 наиболее заметно пересекает территории Франции, Германии, Польши и Финляндии. Наконец, Англия практически поровну делится между Римлендом 2 и Римлендом 3.
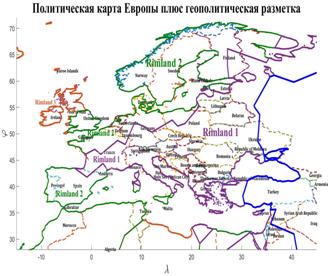
Рис.32. Политическая карта Европы плюс геополитическая разметка
Продолжим в принятой выше терминологии изучение вопроса о наличии (отсутствии) геополитических разломов. Обратим внимание на Африку. Соберем вместе политическую карту Африки и проведем геополитические линии, перечень которых приведен на рис.30. На рис.33 приведена итоговая карта для Африки.
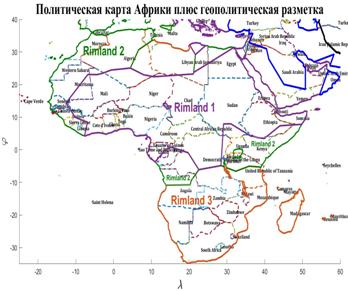
Рис.33. Политическая карта Африки плюс геополитическая разметка
Общий осмотр карты рис.33 говорит о том, что государственные границы отдельных стран на африканском континенте и геополитические линии заметно не согласованы. Более подробное изучение карты показывает следующее. Сомали делится практически пополам линий отделяющей Римленд 1 и Римленд 2. С учетом прошлых и текущих внутри сомалийских обстоятельств можно считать линию, отделяющую Римленд 1 и Римленд 2 в качестве геополитического разлома. Демократическая республика Конго, Алжир, Ливийская Арабская Джамахирия объединяют территории из трех геополитических классов: Римленд 1, Римленд 2 и Римленд 3. Через Габон, Конго, Кот-д Ивуар, Гвинею, Мавританию, Египет проходит линия, отделяющая Римленд 1 и Римленд 2, а через Анголу — Римленд 2 и Римленд 3.
В связи с анализом расположения геополитических линий на Северной и Южной Америках (рис.30) отметим, что оснований считать их геополитическими разломами пока нет. Если что-то негативное в геополитическом смысле слова и произойдет так это, по всей видимости, будет иметь отношение к линии, разделяющей Римленд 2 и Римленд 3 на северо-западе Северной Америки. Остальные геополитические линии не являются разломами в том числе и потому, что соседние территории имеют единое морское позиционирование.
11. Итоги оптимизации транспортных затрат
Перейдем к завершающей задаче минимизации транспортных затрат для числа точек, равного 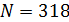 . В качестве начальных значений 318-и точек выберем положения крупнейших городов из имеющейся базы данных. Изучим вопрос о геометрии оптимального позиционирования точек в пределах суши в контексте дихотомии “море – континент”. В этой связи решим три задачи оптимального позиционирования точек: . В качестве начальных значений 318-и точек выберем положения крупнейших городов из имеющейся базы данных. Изучим вопрос о геометрии оптимального позиционирования точек в пределах суши в контексте дихотомии “море – континент”. В этой связи решим три задачи оптимального позиционирования точек:
1) чисто морской тип транспортировки грузов, когда затраты на перевозку грузов морем равны нулю, 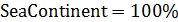 ; ;
2) чисто континентальный тип транспортировки грузов, когда затраты на перевозку грузов по суше равны нулю, 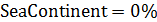 ; ;
3) смешанный тип транспортировки грузов, когда затраты на перевозку грузов по морю и по суше сравнимы, например, следуя (52) — (53¢), будем считать, что 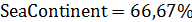 . .
Отметим, что, с точки зрения здравого смысла, первая и вторая задачи невозможны в реальности, поскольку затраты на транспорт минимизируются, но всегда остаются ненулевыми для любого вида транспорта. Однако решение этих задач важно для осознания решения третьей задачи в терминах дихотомии “море – континент”. Согласно (52) условие обнуления затрат на транспорт морем сводится к условию 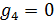 , аналогично обнуление затрат на транспорт по суше сводится к условиям: , аналогично обнуление затрат на транспорт по суше сводится к условиям: 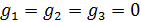 . .
Чтобы представить в общих чертах решения первой и второй задач, необходимо принять во внимание, введенную ранее минимаксную транспортную доктрину. Пусть транспортные затраты морем равны нулю, в этом случае необходимо представить географическую карту мира без океанов, т.е. остается только суша, в рамках которой согласно минимаксной транспортной доктрине точки максимально удаляются друг от друга с учетом неоднородности распределения плотности емкости среды обитания. Если транспортные затраты по суше равны нулю, необходимо представить географическую карту мира без континентов, тогда для позиционирования точек остается только береговая линия, по которой они равномерно распределяются с учетом неоднородности плотности емкости среды обитания. Таким образом, морской тип транспортных коммуникаций способствует продвижению точек внутрь континентов и, наоборот, континентальный тип транспортных коммуникаций продвигает точки ближе к береговой линии. Представленные выводы в краткой метафорической форме можно свести к формуле взаимопроникновения моря и суши: “море  континент”. континент”.
Решим первую задачу, когда считается, что затраты на перевозку грузов морем равны нулю, т.е. 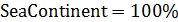 . На рис.34 приведен итог оптимизации 318-и точек в первой задаче. В качестве параметров процедуры оптимизации, рассмотренной в разделе №9, выбирались следующие значения: . На рис.34 приведен итог оптимизации 318-и точек в первой задаче. В качестве параметров процедуры оптимизации, рассмотренной в разделе №9, выбирались следующие значения: 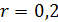 ; ; 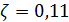 ; ; 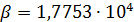 ; ;  ; ; 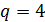 ; ; 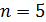 , , 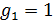 , , 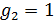 , , 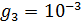 , , 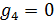 . Первоначально позиции точек совпадали с позициями 318-и городов. Для достижения оптимума в рамках данной процедуры потребовалось 30 шагов и один пересчет емкостей среды обитания каждой из точек. . Первоначально позиции точек совпадали с позициями 318-и городов. Для достижения оптимума в рамках данной процедуры потребовалось 30 шагов и один пересчет емкостей среды обитания каждой из точек.
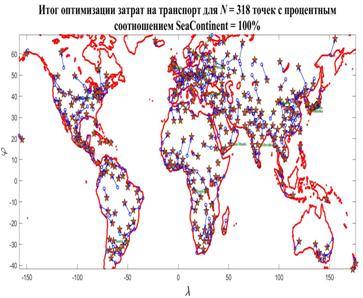
Рис.34. Итог оптимизации затрат на транспорт для  точек с процентным соотношением точек с процентным соотношением 
На рис.34 центрами маркеров в виде синих окружностей (o) отвечены исходные позиции точек. Центры маркеров в виде пентаграмм обозначают позиции точек после минимизации транспортных затрат. В итоге процедуры оптимизации суммарные затраты на транспорт уменьшились на 39,6% и составили 6,6% от суммарной емкости среды обитания. На рис.34 названиями городов отмечены пентаграммы в количестве 13, позиции которых находились в пределах  углового расстояния от одного из городов исходного перечня. Стрелками обозначены переходы от исходных позиций к оптимальным, когда угловое расстояние превышало значение углового расстояния от одного из городов исходного перечня. Стрелками обозначены переходы от исходных позиций к оптимальным, когда угловое расстояние превышало значение 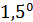 . .
Изучение оптимальных позиций точек на рис.34 недвусмысленно демонстрирует передвижение точек внутрь континентов, что соответствует действию минимаксной транспортной доктрины.
Перейдем к решению второй задачи, когда считается, что затраты на перевозку грузов по суше равны нулю, т.е. 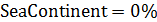 . На рис.35 приведен итог оптимизации 318-и точек во второй задаче. В качестве параметров процедуры оптимизации выбирались следующие значения: . На рис.35 приведен итог оптимизации 318-и точек во второй задаче. В качестве параметров процедуры оптимизации выбирались следующие значения: 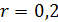 ; ;  ; ; 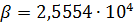 ; ; 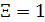 ; ; 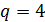 ; ; 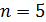 , , 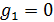 , , 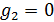 , , 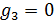 , , 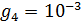 . Первоначально позиции точек совпадали с позициями 318-и городов. Для достижения оптимума в рамках данной процедуры потребовалось 40 шагов и три пересчета емкостей среды обитания каждой из точек. . Первоначально позиции точек совпадали с позициями 318-и городов. Для достижения оптимума в рамках данной процедуры потребовалось 40 шагов и три пересчета емкостей среды обитания каждой из точек.
На рис.35 центрами маркеров в виде синих окружностей (o) отвечены исходные позиции точек. Центры маркеров в виде пентаграмм обозначают позиции точек после минимизации транспортных затрат. В итоге процедуры оптимизации суммарные затраты на транспорт уменьшились на 9,4% и составили 16,8% от суммарной емкости среды обитания. На рис.35 названиями городов отмечены пентаграммы в количестве 57, позиции которых находились в пределах 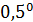 углового расстояния от одного из городов исходного перечня. углового расстояния от одного из городов исходного перечня.
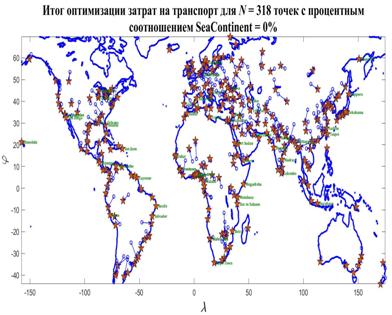
Рис.35. Итог оптимизации затрат на транспорт для 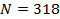 точек с процентным соотношением точек с процентным соотношением 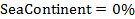
Изучение оптимальных позиций точек на рис.35 демонстрирует очевидное передвижение точек ближе к береговой линии в соответствие с действием минимаксной транспортной доктрины для данного случая. К сожалению, имеющиеся вычислительные ресурсы не позволили использовать алгоритм оптимизации предыдущего раздела при более продвинутых значениях параметров ( ), что обеспечило бы передвижение всех точек к береговой линии. ), что обеспечило бы передвижение всех точек к береговой линии.
В контексте описания в общих чертах решений первой и второй задач становится понятным смысл решения третьей задачи, которая имеет непосредственное отношение к реальности. В случае ненулевых затрат на транспорт, как по морю, так и по суше, вид распределения точек похож на нечто среднее между морским и континентальным типами позиционирования точек первых двух задач. В качестве примера рассмотрим промежуточный тип, когда процентное соотношение выбирается равным 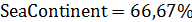 , а транспортные параметры согласно (52) — , а транспортные параметры согласно (52) —  — —  , ,  , , 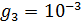 , ,  . .
На рис.36 приведен итог оптимизации затрат на транспорт для 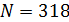 точек, исходное расположение которых совпадало с положением крупнейших городов из имеющейся базы данных. В качестве параметров процедуры оптимизации, рассмотренной в разделе №9, выбирались следующие значения: точек, исходное расположение которых совпадало с положением крупнейших городов из имеющейся базы данных. В качестве параметров процедуры оптимизации, рассмотренной в разделе №9, выбирались следующие значения: 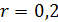 ; ; 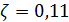 ; ; 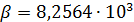 ; ;  ; ; 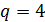 ; ; 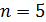 . Для достижения оптимума в рамках данной процедуры потребовалось 27 шагов и два пересчета емкостей среды обитания каждой из точек. На рис.36 центрами маркеров в виде синих окружностей (o) отвечены исходные позиции точек. Центры маркеров в виде пентаграмм обозначают позиции точек после минимизации транспортных затрат. В итоге процедуры оптимизации суммарные затраты на транспорт уменьшились на 7,8% и составили 10,1% от суммарной емкости среды обитания. На рис.36 названиями городов отмечены пентаграммы в количестве 31, позиции которых находились в пределах . Для достижения оптимума в рамках данной процедуры потребовалось 27 шагов и два пересчета емкостей среды обитания каждой из точек. На рис.36 центрами маркеров в виде синих окружностей (o) отвечены исходные позиции точек. Центры маркеров в виде пентаграмм обозначают позиции точек после минимизации транспортных затрат. В итоге процедуры оптимизации суммарные затраты на транспорт уменьшились на 7,8% и составили 10,1% от суммарной емкости среды обитания. На рис.36 названиями городов отмечены пентаграммы в количестве 31, позиции которых находились в пределах 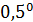 углового расстояния от одного из городов исходного перечня. углового расстояния от одного из городов исходного перечня.
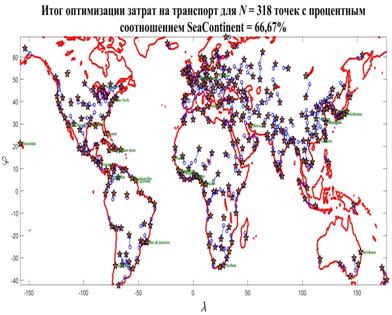
Рис.36. Итог оптимизации затрат на транспорт для  точек с процентным соотношением точек с процентным соотношением 
В результате решения трех упомянутых выше задач оптимального транспортного позиционирования набора точек можно сформулировать следующую общую задачу. Подобрать функционал транспортных издержек, так чтобы оптимальные позиции некоторого набора точек относительно этого функционала соответствовали реальным позициям городов, выступающих в качестве логистических центров. Имеющие у автора на текущий момент времени вычислительные ресурсы недостаточны для решения данной задачи.
12. Заключение
В работе построена математическая модель геополитики. В основу модели положено центральное понятие, названное “емкостью среды обитания”. Данное понятие определено и исчислено. Построена функция плотности емкости среды обитания, зависящая от распределения среднегодовой температуры и осадков на поверхности Земли. Установлена высокая корреляционная связь плотности емкости среды обитания и плотности народонаселения Земли.
Произведена развертка плотности емкости среды обитания по государствам. Среди рекордсменов в убывающей последовательности ожидаемо оказались: Россия, США, Бразилия, Китай, Австралия и т.д. Определен и изучен показатель, имеющий смыл удельной емкости среды обитания в расчете на душу населения. Произведено ранжирование стран и территорий по этому показателю. Особое внимание обращено на соотношение данных показателей отдельных стран по отношению к РФ.
Изучен вопрос о взаимоотношении плотности емкости среды обитания и рельефа. Строятся и сравниваются территории, где сосредоточено 50% народонаселения и 50% емкости среды обитания. Строятся поля градиента плотности емкости среды обитания.
Производится классификация стран и территорий в терминах “высоко – невысоко” и “благоприятно – неблагоприятно”, т.е. в четырех категориях, учитывающих рельеф и плотность емкости среды обитания. Строятся карты территорий всех четырех типов. Вводится и подсчитывается индекс разнообразия отдельных территорий и государств.
Разработан алгоритм по случайному нанесению точек на поверхность суши с учетом плотности емкости среды обитания. Данный алгоритм необходим для разработки решения задачи оптимального позиционирования точек с точки зрения минимизации транспортных затрат между ними.
Формулируется математическая модель транспортных потоков между отдельными точками, выступающими в виде логистических узлов. За основу берется известная гравитационная модель и экспоненциальный тип зависимости от обобщенных расстояний между точками. Вводится минимаксная транспортная доктрина, обеспечивающая при оптимизации позиций точек минимум транспортных издержек при максимуме заполнения среды обитания с учетом неоднородного распределения плотности емкости среды обитания.
Подробно изложена методика подсчета обобщенных расстояний между точками с учетом различия участков, проходящих по суше и по морю. Данные расстояния оцениваются в терминах удельных энергетических затрат по перемещению единицы веса условного груза.
Строится и тестируется алгоритм минимизации транспортных потоков для произвольного набора точек. Данный алгоритм выступает в форме некоторой модификации процедуры градиентного спуска с учетом береговой линии и неодносвязности области определения позиций точек функционала транспортных издержек.
В рамках калькуляции глобального трафика построен специальный показатель под названием процентное соотношение “море – континент”. На основе данного показателя производится классификация точек (территорий) в геополитических терминах. Этот показатель позволил формализовать введение таких хорошо известных в геополитике понятий, как Хартленд и Римленд.
Осуществлено подразделение Хартленда на Хартленд 1 и Хартленд 2. Оказалось, что ядро Харленда именуемое Хартленд 1 состоит из Центральной Азии, Тибета, большей части Китая и части РФ. Если Хартленд и Римленд в геополитике принято относить к “Континенту”, то все остальное относят к “Морю”. Оказалось, что емкости сред обитания территорий, позиционированных в Море и в Континенте приблизительно одинаковы. Территории, позиционированные в Море, были разделены на две группы относительно среднего значения и названы Римленд 3 и Римленд 4. Выявлены города (Окленд и Ланьчжоу) из рассматриваемого перечня, состоящего из 318 городов, имеющие минимальное и максимальное значение процентного соотношения. Проведена полная классификация всех имеющихся точек – городов и соответствующих территорий из принятого перечня в терминах геополитики.
Построены комбинированные глобальная и региональные карты, содержащие политическую и геополитическую разметки. Произведен анализ данных карт на предмет наличия так называемых геополитических “разломов”. О наличии разломов можно говорить в том случае, если некоторые геополитические линии проходят не по границе отдельного государства, а по его территории, глубоко в нее вклиниваясь.
В рамках решения задачи минимизации транспортных издержек было рассмотрено 318 точек, начальное расположение которых совпадало с положением 318-и крупнейших городов на Земле. В едином комплексе численно решались три подзадачи. При решении каждой из трех подзадач критическим было наличие минимаксной транспортной доктрины. В первой подзадаче считалось, что издержки на транспорт по морю равны нулю; во второй задаче считалось, что издержки на транспорт по суше равны нулю и, наконец, в третьей подзадаче были выбраны реальные значения затрат на транспорт. Показано, что оптимальная конфигурация точек третьей подзадачи представляет собой нечто среднее из оптимальных конфигураций первых двух подзадач.
References
1. Plokhotnikov K.E. Normativnaya model' global'noi istorii. — M.: Izd-vo MGU, 1996. 64s.
2. Plokhotnikov K.E. Eskhatologicheskaya strategicheskaya initsiativa: Istoricheskii, politicheskii, psikhologicheskii i matematicheskii kommentarii.— M.: Izd-vo MGU, 2001. 182s.
3. Plokhotnikov K.E. Eskhatologicheskaya strategicheskaya initsiativa: istoricheskii, politicheskii, psikhologicheskii i matematicheskii kommentarii. – 2-e izd., pererab. i dop. — M.: Goryachaya liniya – Telekom, 2014. 251c.
4. http://climate.geog.udel.edu/~climate/html_pages/download.html#lw_temp2
5. http://climate.geog.udel.edu/~climate/html_pages/README.lw2.html
6. http://neo.sci.gsfc.nasa.gov/view.php?datasetId=SEDAC_POP
7. http://thematicmapping.org/downloads/world_borders.php
8. Shvetsov V.I. Matematicheskoe modelirovanie transportnykh potokov// Avtomat. i telemekh., 2003, Vyp. 11, s. 3 — 46.
9. Vvedenie v matematicheskoe modelirovanie transportnykh potokov: ucheb. posobie / Gasnikov A.V., Klenov S.L., Nurminskii E.A., Kholodov Ya.A. i dr. Pod red. A.V. Gasnikova. — M.: MFTI, 2010. 362s.
10. Zhinkin V.B., Kachanov I.V., Tovstykh I.E. Teoriya korablya. Khodkost' sudna: metodicheskoe posobie dlya provedeniya prakticheskikh zanyatii po distsipline “Teoriya korablya”. — Mn.: BNTU, 2009. 54s
Link to this article
You can simply select and copy link from below text field.
|




